乐理
音乐基础不牢。
声音的频率
声音是由声源振动产生的，通过机械波传递。
声音的频率就是机械波的频率，也是声源振动的频率。
比如声源振动 \(440\) 次每秒，频率就是 \(440\mathrm{Hz}\)。“每秒” 这个单位 \(\mathrm{s^{-1}}\) 也记作赫兹 \(\mathrm{Hz}\)，是国际单位制 “秒” 的导出单位。
钢琴琴键的声音频率
规定一个基准频率，比如 \(440\mathrm{Hz}\)，作为第一个音。
把第一个音的频率乘上 \(\sqrt[12]{2}\)，就得到第二个音。一直乘，乘了十二次之后，第十三个音的频率正好是第一个音频率的两倍。
这十三个音把一个 \(1:2\) 的频率区间分成了十二个部分，每个音的频率都是对应部分的端点，相邻两音的频率比为 \(1:\sqrt[12]{2}\)。这就是十二平均律。
如果把第一个音（\(440\mathrm{Hz}\)）记作
A4，往前乘十二次，得到 \(880\mathrm{Hz}\) 的音，就记作A5。同理，再乘十二次，得到 \(1760\mathrm{Hz}\) 就是A6。还可以往后除，\(220\mathrm{Hz}\) 是
A3，\(110\mathrm{Hz}\) 是A2。同理。\(27.5\mathrm{Hz}\) 是
A0，\(3520\mathrm{Hz}\) 是A7。A7再往前乘三次，得到频率为 \(3520 \times \sqrt[4]{2} \mathrm{Hz}\) 的音，记作C8。从
A0到C8，有 88 个音，频率构成首项为 \(27.5\)，公比为 \(\sqrt[12]{2}\) 的等比数列。这就是 88 键钢琴每个琴键的频率。
上面是规定 \(\mathrm{A4=440Hz}\) 时，还可以有其他规定。
音程
两个音之间的频率比，称为音程。
频率比为 \(1:2\) 的两个音之间，音程称为一个纯八度（简称八度）。
快速认识钢琴一个八度里的音：
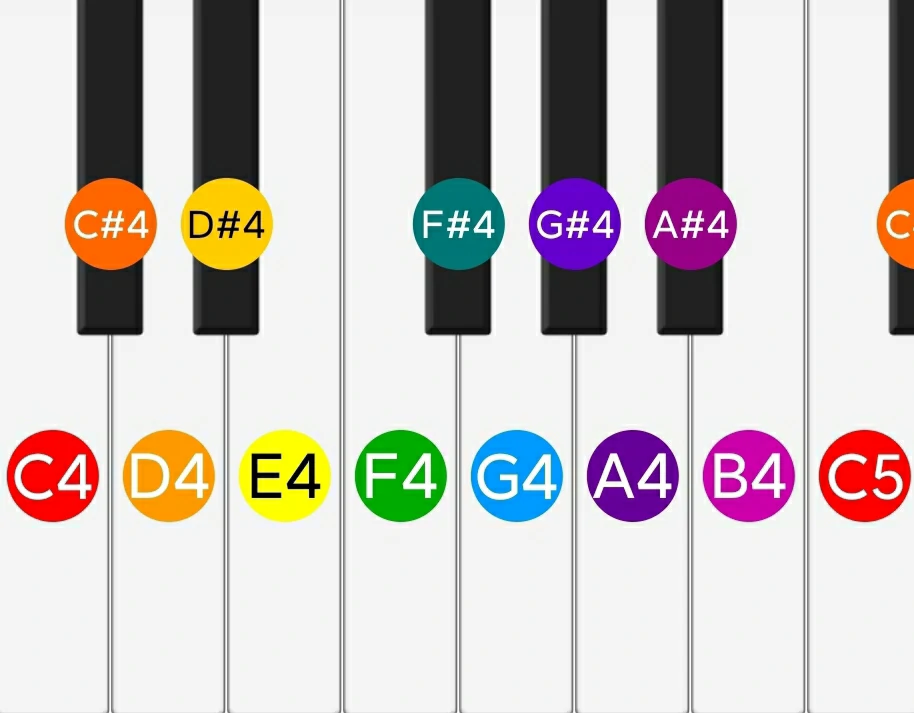
两个相邻琴键的频率比，比如 C4 和 C#4 之间，频率比为
\(1:\sqrt[12]{2}\)，称为一个半音。也叫小二度。
两个琴键相隔一个琴键的频率比，比如 C4 和 D4 之间，频率比为
\(1:\sqrt[6]{2}\)，称为两个半音。也叫一个全音或大二度。
音程速查表
一四五八无大小，二三六七没有纯。
P1、P8、P4、P5 是完全协和音程。
M3、m3、M6、m6 是不完全协和音程。
另外的是不协和音程。
| 相隔半音数 | 音程名（P） | 音程名（M） | 音程名（m） | 音程名（增） | 音程名（减） |
|---|---|---|---|---|---|
| 0 | 纯一度 P1 | 减二度 | |||
| 1 | 小二度 | 增一度 | |||
| 2 | 大二度 | 减三度 | |||
| 3 | 小三度 m3 | 增二度 | |||
| 4 | 大三度 M3 | 减四度 | |||
| 5 | 纯四度 P4 | 增三度 | |||
| 6 | 增四度 | 减五度 | |||
| 7 | 纯五度 P5 | 减六度 | |||
| 8 | 小六度 m6 | 增五度 | |||
| 9 | 大六度 M6 | 减七度 | |||
| 10 | 小七度 | 增六度 | |||
| 11 | 大七度 | 减八度 | |||
| 12 | 纯八度 P8 | 增七度 |
小某度 + 小二度 = 大某度
大 / 纯某度 + 增一度 = 增某度
小 / 纯某度 - 增一度 = 减某度
二度 + 二度的情况包括但不限于：
- 小二度 + 小二度 = 大二度
- 大二度 + 大二度 = 大三度
- 大二度 + 小二度 = 纯四度
三度 + 三度 = 五度的情况包括但不限于：
- 大三度 + 小三度 = 纯五度
- 大三度 + 大三度 = 增五度
- 小三度 + 小三度 = 减五度
五度 + 三度 = 七度的情况包括但不限于：
- 纯五度 + 大三度 = 大七度
- 纯五度 + 小三度 = 小七度
- 增五度 + 大三度 = 增七度
- 减五度 + 小三度 = 减七度
和弦
参考音乐词典。
两个及以上的音同时按下去，称为柱式和弦。
最低音称为根音，根音向上 X 度的音称为 X 音，最高音称为冠音。以根音 C 为例：
三和弦
三个大 / 小三度关系的音（根音、三音、五音），根音到冠音是五度（6~8 半音）。
| 名字 | 符号 | 根音到其他音的音程 | 各个组成音之间相隔的半音数 |
|---|---|---|---|
| 大三和弦 | C | 大三度、纯五度 | 7=4+3 |
| 小三和弦 | Cm | 小三度、纯五度 | 7=3+4 |
| 增三和弦 | Caug，C+ | 大三度、增五度 | 8=4+4 |
| 减三和弦 | Cdim，C° | 小三度、减五度 | 6=3+3 |
七和弦
四个三度关系的音（根音、三音、五音、七音），根音到冠音是七度。
可由三和弦再加一个七音得到。
X+5 的意思是把 X 和弦的五音升半音。
| 名字 | 符号 | 三和弦加一个七音 | 各个组成音之间相隔的半音数 |
|---|---|---|---|
| 大七和弦（大大七和弦） | Cmaj7、CM7、CΔ7 | 大三和弦、大七度 | 11=4+3+4 |
| 属七和弦（大小七和弦） | C7 | 大三和弦、小七度 | 10=4+3+3 |
| 小大七和弦 | CmM7 | 小三和弦、大七度 | 11=3+4+4 |
| 小七和弦（小小七和弦） | Cm7 | 小三和弦、小七度 | 10=3+4+3 |
| 增大七和弦 | CM7+5 | 增三和弦、大七度 | 11=4+4+3 |
| 增小七和弦 | Caug7，C7+5 | 增三和弦、小七度 | 10=4+4+2 |
| 导七和弦（减小七和弦） | Cm7-5 | 减三和弦、小七度 | 10=3+3+4 |
| 减七和弦（减减七和弦） | Cdim7，C°7 | 减三和弦、减七度 | 9=3+3+3 |
其他
| 名字 | 符号 | 根音到其他音的音程 | 各个组成音之间的音程 |
|---|---|---|---|
| 强力和弦 | C5 | 纯五度 | 7 |
| 大六和弦 | C6 | 大三和弦 + 大六度 | 4+3+2 |
| 小六和弦 | Cm6 | 小三和弦 + 大六度 | 3+4+2 |
升降号
\(\sharp\) 为升号（sharp），用于把一个音升高半音。
比如 \(\mathrm{B \sharp 4 =
C5}\)。B#4 = C5
\(\flat\) 为降号（flat），用于把一个音降低半音。
比如 \(\mathrm{D \flat 4 = C \sharp
4}\)。Db4 = C#4
音名和唱名
音名（pitch name，音高名称）
C4、C#4、D4等是音名，对应绝对音高。比如 \(\mathrm{C4 = 220 \times \sqrt[4]{2} Hz}\)。
唱名（sol-fa note，唱名表示法 1 中的音符）
do、re、mi、fa、sol、la、ti是唱名，对应相对音高。在简谱里记作
1、2、3、4、5、6、7。我们可以规定
1至7分别对应七个白键C4至B4。这时简谱头部会有 \(\mathrm{1 = C}\)。在简谱里，如果用 \(1\) 表示 \(\mathrm{C4}\)，那么 \(\mathrm{\dot{1}}\) 就表示 \(\mathrm{C5}\)。\(\mathrm{\dot{\dot{1}}}\) 表示 \(\mathrm{C6}\)，\(\underset{·}{1}\) 表示 \(\mathrm{C3}\)，以此类推。
音阶
在音乐理论中，音阶（scale，尺度）是按基本频率或音高排序的任何一组音符。按音高递增排序的音阶是升序音阶，按音高递减排序的音阶是降序音阶。2
A0 B0 C1 D1 E1 F1 G1 A1 B1 ... C4 D4 E4 F4 G4 A4 B4 ... C7 D7 E7 F7 G7 A7 B7 C8
就是一组升序音阶，对应钢琴的所有白键。
在上面的例子中，每个八度里用到了七个音名 C D E F G A B（不包括区间右端点），这被称为七声音阶（heptatonic
scale）。
音级
七声音阶里有七个音级（degree，刻度）：
| 音级 | 名称 | 英文名称 |
|---|---|---|
| \(Ⅰ\) | 主音 | tonic |
| \(Ⅱ\) | 上主音 | supertonic |
| \(Ⅲ\) | 中音 | mediant |
| \(Ⅳ\) | 下属音 | subdominant |
| \(Ⅴ\) | 属音 | dominant |
| \(Ⅵ\) | 下中音 | submediant |
| \(Ⅶ\) | 导音 | subtonic / leading note |
属 = 五
【音阶相同】是什么意思
\(\mathrm{C-D-E-F-G-A-B}\) 和
\(\mathrm{A-B-C-D-E-F-G}\) 音阶相同吗？
这两组音阶分别都是同一个八度里的音（不包括右端点）。
如果把 “音阶” 理解为【无限扩展到多个八度后，所有音的绝对音高】的话，得到的答案是相同的，因为【它们都使用了钢琴的所有白键】。
但是看别人网上的回答，这两组音阶是不同的。
原因在于：
首先，主音不同。 前者以 \(\mathrm{C}\) 为主音，后者以 \(\mathrm{A}\) 为主音。
其次，音级之间的音程关系（相隔的半音数）不同。
前者为 \(2-2-1-2-2-2-1\)，
后者为 \(2-1-2-2-1-2-2\)。（算上下一个八度里的主音）
我们说两组音阶相同，意思是它们的主音、音程关系都相同。
调式
狭义的调式（mode） = 主音 + 音程关系
- 确定一个起始音（主音）。
- 从主音开始，往后（高音方向）取不同的音级。这些不同的音相隔的半音数可能不同，直到取完一个八度。
- 再往前、往后取，直到取完所有八度。
比如：
- 以 \(\mathrm{C}\)
为主音，音程关系为 \((2-2-1-2-2-2-1)\)
的调式，称为 \(\mathrm{C}\)
自然大调。
C Major用到的音名为： \[ \mathrm{...B3-C4-D4-E4-F4-G4-A4-B4-C5...} \] - 以 \(\mathrm{A}\)
为主音，音程关系为 \((2-2-1-2-2-2-1)\)
的调式，称为 \(\mathrm{A}\)
自然大调。
A Major用到的音名为： \[ \mathrm{...G\sharp3-A4-B4-C\sharp4-D4-E4-F\sharp4-G4\sharp-A5...} \] - 以 \(\mathrm{A}\)
为主音，音程关系为 \((2-1-2-2-1-2-2)\)
的调式，称为 \(\mathrm{A}\)
自然小调。
A Minor用到的音名为： \[ \mathrm{...G3-A4-B4-C4-D4-E4-F4-G4-A5...} \]
移调
移调（transpose）就是把所有音同时升高或降低相同的半音数。
移调前后，所有音的相对间隔不变。即音程关系不变。
中古调式
7 种中古调式（church mode，教会调式）是指广义的调式，只确定了音程关系，还没确定主音。
即确定了主音-上主音-中音-下属音-属音-下中音-导音-主音之间相隔的半音数。
| 调式名 | 别名 / 结构相同的调式 | 相隔的半音数 |
|---|---|---|
| 伊奥尼亚调式 Ionian mode |
自然大调Major中国七声清乐宫调 |
2-2-1-2-2-2-1 |
| 多利亚调式 Dorian mode |
中国七声清乐商调 | 2-1-2-2-2-1-2 |
| 弗里几亚调式 Phrygian mode |
中国七声清乐角调 | 1-2-2-2-1-2-2 |
| 利底亚调式 Lydian mode |
2-2-2-1-2-2-1 |
|
| 混合利底亚调式 Mixolydian mode |
中国七声清乐徵调 | 2-2-1-2-2-1-2 |
| 爱奥尼亚调式 Aeolian mode |
自然小调Minor中国七声清乐羽调 |
2-1-2-2-1-2-2 |
| 洛克里亚调式 Iocrian mode |
1-2-2-1-2-2-2 |
在确定了主音之后，就是狭义的 \(7 \times 12\) 种调式。因为一个八度里的 \(12\) 个音每一个都可以作为主音。
比如以 \(\mathrm{C}\)
为主音的伊奥尼亚调式，就叫 C Ionian、
C Major、“\(\mathrm{C}\)
自然大调” 或者 “\(\mathrm{C}\)
大调”。
不同的中古调式可能使用相同的琴键
仔细观察 7 种中古调式，你会发现【相邻音级之间相隔的半音数】在这 7 种调式里是一个循环。
- 2-2-1-2-2-2-1
- 2-1-2-2-2-1-2
- 1-2-2-2-1-2-2
- 2-2-2-1-2-2-1
- 2-2-1-2-2-1-2
- 2-1-2-2-1-2-2
- 1-2-2-1-2-2-2
因此，如果以 \(\mathrm{X}\) 为主音，构造自然大调音阶的话（加数字表示升高半音数）：
以 \(\mathrm{Y=(X+2)}\) 为主音，构造出多利亚调式的音阶，与 \(\mathrm{X}\) 自然大调使用的琴键相同。
以 \(\mathrm{Z=(X+2+2)}\) 为主音，构造出弗里几亚调式的音阶，与 \(\mathrm{X}\) 自然大调、\(\mathrm{Y}\) 多利亚调使用的琴键相同。
……
以 \(\mathrm{V=(X+2+2+1+2+2)}\) 为主音，构造出自然小调的音阶，与 \(\mathrm{X}\) 自然大调、\(\mathrm{Y}\) 多利亚调、\(\mathrm{Z}\) 弗里几亚调…… 使用的琴键相同。
以 \(\mathrm{W=(X+2+2+1+2+2+2)}\) 为主音，构造出洛克里亚调式的音阶，与 \(\mathrm{X}\) 大调、\(\mathrm{Y}\) 多利亚调、\(\mathrm{Z}\) 弗里几亚调…… \(\mathrm{V}\) 自然小调使用的琴键相同。
调式音阶
调式音阶为主音 + 音程关系。如：
C 大调音阶为：\(\mathrm{C-D-E-F-G-A-B}\)
A 小调音阶为：\(\mathrm{A-B-C-D-E-F-G}\)
它们使用的绝对音名相同，叫关系大小调。
调内和弦
以 C 大调上的三和弦为例，它是在 C 大调音阶上取三个三度关系的音级构成和弦。
有七个音级，每个都可以作为根音，于是七个和弦分别为：
C Dm Em F G Am B°
类似地，所有大调的七个三和弦都是【大 - 小 - 小 - 大 - 大 - 小 - 减】，因为：
- 2-2-1-2-2-2-1
- (2+2)+(1+2)=(4+3)= 大三和弦
- (2+1)+(2+2)=(3+4)= 小三和弦
- ……
- (1+2)+(2+1)=(3+3)= 减三和弦
- 以此类推
在一级、四级、五级上（以它们为根音）的和弦都是大三和弦，也叫主和弦、下属和弦、属和弦。它们叫大调上的正三和弦，另外四个叫大调上的副三和弦。
类似地，小调的各级三和弦为：【小 - 减 - 大 - 小 - 小 - 大 - 大】。这和小调相对于大调的音程关系看起来类似，都是把大调的 6 当成小调的 1。
大调的各级七和弦为：【大 - 小 - 小 - 大 - 属 - 小 - 导】。
五度圈
Father Charles Goes Down And Ends Battle
4-1-5-2-6-3-7
在钢琴上以 C 为起点依次向后取（上行）纯五度关系的音：
C -> G -> D -> A -> E -> B -> F#/Gb -> Db/C# -> Ab -> Eb -> Bb -> F -> C
最后又回到了 C，且这一圈里包含了十二个完整的音名。
五度圈里顺时针上行是纯五度关系，逆时针上行 / 顺时针下行是纯四度关系。
和弦的功能
以大调为例。参考常用和弦功能解析全在这了，附实用图表！
主功能组 Tonic
一级和弦用于平稳地开始和结束。
六级或三级和弦用于主的延续向后发展。
属功能组 Dominant
五级或七级和弦用于向主回归。
下属功能组 Subdominant
四级和弦：大的要来了，但是还没来。
二级和弦：251
律式与调式的区别
律式是给乐器调音用的。
在古代，并不能精确测得乐器的音高，所以要取一个能代表标准音高的东西，比如竹管。
竹管越长、吹时的震动频率越低、音高越低。
竹管越短、吹的震动频率越高、音高越高。
取不同长度的竹管作为音名。乐器调音完，有了音名之后，在此基础上进行演奏。
不同地区的演奏者喜欢使用不同长度、不同数目的竹管。比如笔者喜欢使用一些竹管，把它们取名为：
\[ \mathrm{...G3、A3、}\mathbf{C4、D4、E4、G4、A4、}\mathrm{C5、D5...} \]
\(\mathrm{X \in \{C,D,E,G,A\}}\)，其中 \(\mathrm{Xn}\) 竹管的长度是 \(\mathrm{X(n+1)}\) 竹管长度的两倍，竹管越长音高越低。
笔者把使用次数最多的竹管 \(\mathrm{C4、C5...}\) 叫主音 \(\mathrm{C}\)。
\(\mathrm{C、D、E、G、A}\)
就是笔者的五个音级，对应唱名宫、商、角、徵、羽，do
re mi sol la 或者
\(1、2、3、5、6\)。
这一些竹管之间，音程关系为 \(2-2-3-2-3\)。还可以往频率高、低的方向继续加竹管，并保持主音和音程关系不变，这就是笔者的调式。
即：
- 律式规定了：【音名】<->【频率】的对应关系
- 调式规定了：【唱名】<->【音名】的对应关系
三分损益法
三分损益法定音取的是 单位长度 的竹管，所以宫、商、角、徵、羽是 唱名。
- 取一个 \(81\) 个单位长度的定音竹管，作为宫。
- 截断（损）三分之一，剩余的三分之二（\(81 \times \frac{2}{3} = 54\)）作为徵。
- 再加长（益）三分之一，\(54 \times \frac{4}{3} = 72\)，作为商。
- 再损三分之一，\(72 \times \frac{2}{3} = 48\)，作为羽。
- 再益三分之一，\(48 \times \frac{4}{3} = 64\)，作为角。
| 唱名 | 宫 | 商 | 角 | 徵 | 羽 |
|---|---|---|---|---|---|
| 单位长度 | \(81\) | \(72\) | \(64\) | \(54\) | \(48\) |
十二律
\[ \left\{ \begin{aligned} 64 \times \frac{2}{3} & = 42\frac{2}{3} \\ 42\frac{2}{3} \times \frac{4}{3} & = 56\frac{8}{9} \\ 56\frac{8}{9} \times \frac{4}{3} & = 75\frac{23}{27} \\ 75\frac{23}{27} \times \frac{2}{3} & = 50\frac{46}{81} \\ \vdots \end{aligned} \right. \]
在上面的基础上继续损益，注意在 \(42\frac{2}{3}\) 处益了两次，然后继续损 — 益 — 损 — ……
并规定 宫 = 黄钟，相当于十二平均律简谱的 \(\mathbf{1=C}\)，得到十二律的各个音：
| 序号 | 音名 | 来源 | 去向 | 单位长度 |
|---|---|---|---|---|
| 1 | 黄钟 | 起始音 | 损，林钟 | \(81\) |
| 2 | 大吕 | 蕤宾，益 | 损，夷则 | \(75\frac{23}{27}\) |
| 3 | 太簇 | 林钟，益 | 损，南吕 | \(72\) |
| 4 | 夹钟 | 夷则，益 | 损，无射 | \(67\frac{103}{243}\) |
| 5 | 姑洗 Xiǎn | 南吕，益 | 损，应钟 | \(64\) |
| 6 | 仲吕 | 无射，益 | 损，清黄钟 | \(59\frac{2039}{2187}\) |
| 7 | 蕤宾 | 应钟，益 | 益，大吕 | \(56\frac{8}{9}\) |
| 8 | 林钟 | 黄钟，损 | 益，太簇 | \(54\) |
| 9 | 夷则 | 大吕，损 | 益，夹钟 | \(50\frac{46}{81}\) |
| 10 | 南吕 | 太簇，损 | 益，姑洗 | \(48\) |
| 11 | 无射 Yì | 夹钟，损 | 益，仲吕 | \(44\frac{692}{729}\) |
| 12 | 应钟 | 姑洗，损 | 益，蕤宾 | \(42\frac{2}{3}\) |
| 13 | 清黄钟 | 仲吕，损 | …… | \(39\frac{6265}{6561}\) |
另外，可以在中国国家数字图书馆查看不同版本的《史记》，宫、商、角、徵、羽对应的音名是不一样的。但如果认为以下几点同时成立的话，便可以推出 {宫，商，角，徵，羽} 对应 {黄钟，太簇，姑洗，林钟，南吕}：
- {黄钟，大吕，太簇，夹钟，姑洗，仲吕，蕤宾，林钟，夷则，南吕，无射，应钟} 的音高顺序是正确的，从低音到高音。
- 可以把第一条集合里的音类比成十二平均律的一个八度内的音名（绝对音高）。
- 可以把 {宫，商，角，徵，羽，宫，...} 类比成十二平均律的唱名（相对音高）。
- 第三条集合里的音，音程关系始终是 \(2-2-3-2-3\)。
- 令宫 = 黄钟。
参考
[1] 维基百科. 十二律 [EB/OL].(2023-07-14)[2023-09-02]. https://zh.wikipedia.org/zh-cn/ 十二律.
[2] 司马迁. 史记：卷二十五 律書第三 [M/OL].(2020-09-10)[2023-09-02]. https://zh.wikisource.org/wiki/ 史記 / 卷 025.
[3] leeonix. 【科普向】中国古代的十二律以及十二平均律 [EB/OL].(2019-07-30)[2023-09-02]. https://www.bilibili.com/read/cv3194623.