过去的笔记
JSON
json 是一个文本文件或者字符串,它的字符具有特定的格式,这个文件可以与程序设计语言里的对象互相转化。
JS:
1 | jsonStr = JSON.stringify(jsObj); |
Python:
1 | import json |
给 VM 里的 Ubuntu 扩容
层次(空间缝隙)
/dev/sda:大概是 VM 设置里分配的硬盘空间大小/dev/sda1:bios_grub/dev/sda2:/boot- 物理卷 pv:
/dev/sda3- 逻辑卷 lv:
- 文件系统
/dev/mapper/ubuntu--vg-ubuntu--lv->/dev/dm-0
- 文件系统
- 逻辑卷 lv:
需求:
先扩 sda
从 sda 向 sda3 匀
从 sda3 向 lv 匀
给 VM 的虚拟磁盘扩容
关机状态下:编辑虚拟机设置 -> 硬盘 -> 扩展
从 sda 向 sda3 匀
1
sudo parted
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22GNU Parted 3.4
Using /dev/sda
Welcome to GNU Parted! Type 'help' to view a list of commands.
(parted) print all
// 输出……
(parted) print free
Model: VMware, VMware Virtual S (scsi)
Disk /dev/sda: 32.2GB
Sector size (logical/physical): 512B/512B
Partition Table: gpt
Disk Flags:
Number Start End Size File system Name Flags
17.4kB 1049kB 1031kB Free Space
1 1049kB 2097kB 1049kB bios_grub
2 2097kB 1904MB 1902MB ext4
3 1904MB 21.5GB 19.6GB
21.5GB 32.2GB 10.7GB Free Space
(parted) resizepart 3
End? [21.5GB]? 32.3GB //在后面输入扩到的 End,比 End 略大就是扩到底扩完后,
sudo pvs出的 /dev/sda3 会比lsblk出的 sda3 小,执行:1
sudo pvresize /dev/sda3
从 sda3 向 lv 匀
1
sudo lvresize -l +100%FREE /dev/mapper/ubuntu--vg-ubuntu--lv
扩完后,
df -h出的 /dev/mapper/ubuntu--vg-ubuntu--lv 还没变,执行:1
sudo resize2fs /dev/mapper/ubuntu--vg-ubuntu--lv
计算机网络
接网线头的流程和注意事项
RJ45 水晶头的接线方式有两种,多使用 T568B:橙白 | 橙、绿白 | 蓝、蓝白 | 绿、棕白 | 棕。
- 用网线钳的圆孔把网线的表皮剥开,转一下不要使太大力
- 露出来里面的线的长度长一点,比两倍水晶头的长度长
- 你会看到有四对缠在一起的线,把它们分开成一根一根的
- 这时候先不用管它们的顺序
- 用力把它们捋直,多捋几次
- 它们缠在一起的时候是:橙白 | 橙、绿白 | 绿、蓝白 | 蓝、棕白 | 棕,接线的时候要把中间两根交换一下位置
- 用网线钳的刀把它们从中间剪断,保证这几根线的末端是平齐的。注意两点:
- 哪里排列地最整齐紧密,就从哪里剪
- 留下的长度不要比一倍水晶头的长度过长,否则露出来的部分容易损坏。这是一个反面的例子:这几根线的下面留得太长了,没还有完全地分开

- 把这几根线插入到水晶头里。注意:水晶头的卡扣是朝下的
- 如果顺利,这八根线会待在它们的八个凹槽里,它们的头上有八个片片
- 把水晶头插入网线钳的槽里,用网线钳用力把这八个片片刺入线的内部,在刺的时候能感受到阻力
- 两头都接好之后,用工具测试是否联通
概述
世界上第一个网页:http://info.cern.ch
RFC 文档:“请求评论”(Request For Comments)的文档,公开发布的互联网建议标准,请求公众评论。最后制定互联网标准 STD。
互联网服务提供者(Internet Service Provider),可以是移动联通电信公司,也可以是非营利组织。主干 ISP:国 | 地区 ISP:省 | 本地 ISP:省以下。两个同级 ISP 交换信息时,可以通过互联网交换点(Internet eXchange Point)IXP,而不必通过上级 ISP。
计算机网络分边缘部分和核心部分。边缘部分是我们所有人直接使用的主机,如手机和电脑。核心部分是除了边缘主机之外的所有硬件设施,如交换机、路由器、网线。接入网是边缘部分向核心部分过渡的部分。
边缘部分的通信分 C/S 模式和 P2P 模式。两者的区别是学生向老师请教题目和学生之间互相讲题,在下载文件之后做不做种。
核心部分的通信:电路交换是提前联系用一辆专车运货;分组交换是把货物拆分成小的快递,再经过各种站点发送出去;报文交换是将货物作为一个整体,通过多个中转站运送。前两者的区别是一手和多手,后两者的区别是切不切片。
分组交换:
- TCP 协议把报文分组,每组写上头部信息。(包裹大包分成小包,写上序号、寄出地和目的地等)
- 通过路由器一级一级地转发到目的地。
gantt
title 分组交换(甘特图)
dateFormat s
axisFormat %S
section 1 号包
从 A 到 B :0, 5s
从 B 到 C :5, 5s
从 C 到 D :10, 5s
section 2 号包
从 A 到 B :5, 5s
从 B 到 C :10, 5s
从 C 到 D :15, 5s
section 3 号包
从 A 到 B :10, 5s
从 B 到 C :15, 5s
从 C 到 D :20, 5s
- 0-5 时间 1 号包裹从 A 站到 B 站
- 5-10 时间 1 号包裹从 B 站到 C 站、2 号包裹从 A 站到 B 站
- 10-15 时间 1 号包裹从 C 站到 D 站、2 号包裹从 B 站到 C 站、3 号包裹从 A 站到 B 站
- 把各个包裹合并。
物理层
RJ45 水晶头的接线方式有两种,多使用 T568B:橙白 | 橙、绿白 | 蓝、蓝白 | 绿、棕白 | 棕。传的是数字信号。
- 物理层之下的传输媒体
- 导引性传输媒体:双绞线、光缆、同轴电缆、架空明线
- 非导引性传输媒体:空气或真空
集线器工作在物理层。
- 通信双方的交互方式
- 单向通信(单工):一段单行道。电视、广播。
- 双向交替通信(半双工):一段有两个车道的马路,但是规定在一边的车道有车正在走时,另一边(相反方向)的车道不能有车走。对讲机。
- 双向同时通信(全双工):一段正常的两个车道的马路。
编码方式:编码的终点是码,即数字信号。
如何把比特和电压互相转换。
1 | 1 1 0 0 1 |
曼彻斯特编码:中心始终跳变
- G.E. Thomas Convention:
- 中心向下跳变,
‾_,1 - 中心向上跳变,
_‾,0 - 简记:下为 1
- 中心向下跳变,
- IEEE 802.3 Convention 和上面的定义相反
差分曼彻斯特编码:中心始终跳变
- G.E. Thomas Convention:
- 左边界无跳变,
1_|_‾‾|‾_
- 左边界有跳变,
0_|‾_‾|_‾
- 简记:左连为 1
- 左边界无跳变,
- IEEE 802.3 Convention 和上面的定义相反
数据链路层
解决三个问题:发出去之后,哪一方接收;传输何时开始,何时结束;判断是否有传输错误
网卡:
- 负责把有线或无线电信号与比特流互转。工作在物理层和数据链路层。
- 与 CPU 和存储器并行通信,与局域网串行通信
- 接收并缓存 MAC 帧,帧的目标地址不是它自己时,或者不符合格式、校验失败时就丢弃
- 安装驱动到操作系统,实现以太网协议
MAC
MAC 地址有 6 个字节。全 1 的地址是广播地址
Windows 查看网络适配器的 MAC 地址:ipconfig /all
- 前三个字节是 IEEE 的注册管理机构分配的,后三个字节是厂家自行分配的
- 第一个字节最低位:0 为单播,1 为多播
透明传输
帧定界符 SOH 0x01、EOT 0x10,转义字符 ESC 0x1B
如果数据长度超过了 MTU,会被分割成多个帧。
下到物理层:在 MAC 帧前面插入 7 字节的前同步码和 1
字节的帧定界符:就是
10101010 10101010 ... 10101010 10101011。交替的 10
用于时钟同步,最后一个字节的最后一个比特变了,告诉接收端,后面的就是 MAC
帧。不用标记帧结束,因为是曼彻斯特编码,一直在跳变,脱离原本的规律了就是帧结束了。
差错检测
比特差错:01 错了。误码率(BER):平均每传送 \(\mathrm{(BER)^{-1}}\) 个比特,会有一个比特出错。
传输差错:接收方没有收到某一个帧,或者收到了重复的帧,或者收到帧的顺序错了
FCS
帧检验序列 Frame Check Sequence,确保无比特差错
- 提前规定冗余码有 3 位
- 提前规定一个除数 \(P\)
,比冗余码的长度多一位,如
1100 - 把待传的数据
1001 0001后边补上冗余码长度个 0,用除数除它 - 不管大小,
1开头就商1,0开头就商0:
1 | 1 |
- 相减,相当于异或
- 继续除,最后的余数
100就是冗余码 - 把冗余码添加到原数据的末尾
CRC
循环冗余检验 Cyclic Redundancy Check
接收方把收到的、经发送方添加了冗余码后的数据再用 \(P\) 去除。传输没出错 -> 余数为零,反之为极大概率。
除数 \(P\)
还有一种记法,叫生成多项式 \(P(X)\):如
1100 记作:\(X^3+X^2\)
交换机
交换机工作在数据链路层,全双工。并且不使用 CSMA/CD 协议,但仍然使用以太网的帧结构。
交换表的结构:MAC 地址、端口号、有效时间、状态标志
源机器发送数据帧 → 交换机记录源 MAC 地址 → 交换机查找目标 MAC 地址 → 如果目标未知,广播数据帧 → STP 确保广播不会形成环路。
交换机分为直通交换和存储转发。直通交换不校验 FCS,直接读 6 字节的目标地址(有时包含前导码)。
以太网
以太网是局域网的一种实现方式,与 Wifi 的区别是后者不用网线。
- DIX Ethernet V2 和 IEEE 802.3 是以太网的协议,使用 CSMA/CD(冲突检测)
- IEEE 802.11 是 Wifi 的协议,使用 CSMA/CA(冲突避免)
局域网共享信道,为避免冲突,可采用静态划分信道(复用)或动态媒体接入控制
以太网 V2 的 MAC 头部:目标 MAC + 源 MAC + 类型 0800【IPv4】/80DD【IPv6】
- MAC 帧的格式
- (带宽为 \(\mathrm{10Mbit/s}\) 的)以太网 V2: \[ 6 + 6 + 2 + (46 \sim 1500) + 4 = (64 \sim 1518) 字节 \] 其中 \(\mathrm{64Byte = \dfrac{51.2 \mu s \times 10Mbit/s}{8bit/Byte}}\),减去 18 字节的首部和尾部后,得到数据部分的最小长度 46 字节。
100BASE-T 以太网:
- 使用双绞线(T),带宽为 100Mbit/s。
- 标准是 IEEE 802.3u,半双工时使用 CSMA/CD 协议,全双工时不使用。
- 争用期为 5.12 μs,帧最小间隔 0.96 μs,是 10 Mbit/s 以太网的十分之一。
网络层
IPv4 分类编址
4 个字节。
- A 类地址:0 + 7 位网络号 + 3 字节主机号,首字节 0 到 127
- B 类地址:10 + 14 位网络号 + 2 字节主机号,首字节 128 到 191
- C 类地址:110 + 21 位网络号 + 1 字节主机号,首字节 192 到 223
主机号全 1 是广播地址,全 0 是该子网。
私有地址:用于局域网(LAN)内部,不可直接在互联网上路由。
- A 类:10.0.0.0 到 10.255.255.255
- B 类:172.16.0.0 到 172.31.255.255
- C 类:192.168.0.0 到 192.168.255.255
无分类编址 CIDR
子网掩码:用于标记用 IP 地址前面的几位来表示网络地址。
子网掩码类似 255.248.0.0
(11111111 11111000 00000000 00000000),即用前面 13
位表示网络地址,后面的位表示主机地址。记作 IP地址/13。
计算
信道长度、带宽和信噪比会影响数据在信道中传输的速率,而信号传播速度(电磁波在介质中的传播速度)不会。
信噪比越大,接收方接收到的信息失真越少。两种表示方式:
- \(\dfrac {S}{N} = \dfrac {信号平均功率}{噪声平均功率} = 10^{\mathrm {dB}/10}\)
- \(\mathrm{dB} = 10 \lg\dfrac{S}{N}\)
计算传输速率时,取奈氏准则和香农公式的结果小的。
Kibi:内存、存储容量,KiB = KB = 1024B
Kilo:网络带宽,K = 1000,国际单位制的词头
\(\mathrm{bit/s}\)
- 速率
- 吞吐量:指实际速率,进量 + 出量。有多条链路时,吞吐量由瓶颈链路决定。
- 某信道的最高速率:时域上的带宽
- 有效数据(速)率:\(\mathrm {\dfrac {数据长度}{发送时间 + RTT}}\)
\(\mathrm{Hz}\)
频域上的带宽 W:信号频率范围的宽度
秒
- 发送时延:网卡发送数据的时间,与信道长度无关。\(\mathrm {\dfrac {bit}{bit/s}} = \dfrac {数据长度}{发送速率}\)
- 传播时延:电磁波在网线或空气中传播的时间。与信道长度有关。\(\mathrm {\dfrac {m}{m/s} = \dfrac {信道长度}{信号传播速率}}\)
- 处理时延:主机或路由器收到分组后,对分组进行处理的时间。
- 排队时延:分组在路由器输入队列和输出队列里排队的时间。
- ……-> 输出排队 -> 发送 -> 传播 -> 输入排队 -> 处理 -> 输出排队……
- RTT:往返时间(Round-Trip Time)
这里忽略了在接收和发送之间的排队时间和处理时间。
gantt
title RTT(甘特图)
dateFormat s
axisFormat %S
section RTT
RTT :3,17s
section A
发送 :0,3s
接收 :17,3s
…… :20,4s
section 传播
从A到B传播 :1,8s
从B到A传播 :11,8s
section B
接收 :7,3s
发送 :10,3s
bit
时延带宽积:\(\mathrm {s \times bit/s = 传播时延 \times 带宽}\)
已经从发送端发出,但尚未到达接收端的比特数。又叫以比特为单位的链路长度。
m/bit
每比特宽度:每个比特在信道中占据的长度。
\[ \begin {aligned} &\mathrm {m/bit = \dfrac {m}{bit} = \dfrac {信道长}{比特数}} \\ &\mathrm {m/bit = \dfrac {m/s}{bit/s} = \dfrac {信道传播速率}{信道当前带宽}} \end {aligned} \]
其他
利用率:\(网络利用率 = 1 - \dfrac {空闲时延}{当前时延}\)
利用率越高,当前时延越大(堵车)。
码元
用来表示码的单个元。类比信号,码就是波形,码元就是在发送和解读波形时,可以分辨的最小单位波形。码元种类数是信号的状态数 \(n = 2^x\)
- 码元对应的比特数 \(x = \log_2(n)\)
- 当 \(0 < x < 1\) 时,一个比特由多个码元表示
比特率和波特
\(\mathrm{bit/s} = 2Wx = 2W\log_2(n)\)
符号速率(码元每秒)也叫波特 Baud
奈奎斯特准则
无噪声低通信道中,保证接收方接收符号不出错时的速率上限为 2W x 码元数,W 为频域带宽 Hz,单位为波特。
香农公式
速率是有极限的,但要信息传输速率低于极限速率,就一定能找到某种方法实现无差错的传输。
香农 — 哈特莱容量定理,考虑到了信道有噪声:
\[ \begin {aligned} 信道极限速率 & = \mathrm {bit/s = Hz \times bit} \\ & = W \log_2 (1 + \dfrac {S}{N}) \\ \end {aligned} \]
正交振幅调制(QAM)
\[ \begin {aligned} 调制后的信号 & = 振幅 \times 载波 (相位) \\ y & = A\sin (\omega x + \phi) \\ \end {aligned} \]
用不同的振幅和相位排列组合,来表示(承载)不同的基带信号,比只调幅 / 只调频 / 只调相的信息密度高。
使用 \(x\) 个振幅和 \(y\) 个相位的 QAM 时,一个码元对应的比特数是 \(\log _2(xy)\) 向上取整。
信道复用
频分复用(FDM):Frequency Division Multiplexing,把一个大频带划分成若干个小频带,把不同的信号分别调制到这些小频带里。
1 | ^频率 |
时分复用(TDM):把时间分割成一个个 TDM 帧,每帧内分为若干个时隙,每个时隙内分别传送不同的信号。相当于 CPU 单核进程并发。每个 TDM 帧内保证每组信号都传了,就是没传也要保留留给它的空时隙。这造成信道利用率不高。
1 | ^频率 |
统计时分复用(STDM):在每个 STDM 帧内,时隙数量小于信号种类数量。为每组信号动态分配时隙,比如 B 信号断了可以先不传它。
有四组信号 ABCD:
1 | ^信号 |
STDM:
1 | ^频率 |
波分复用(WDM):就是光的频分复用,但是用波长表示。
码分复用(CDM):CDMA 通过为每个用户分配一个独特的扩频码来实现信号的分离,这些扩频码之间是正交的。
- 编码:某用户的码元内积扩频码,与其他用户的叠加成混合信号。
- 解码:混合信号内积用户的扩频码,得到一个码元。
计算机组成原理
注意:这里的知识是未经验证的,不一定正确。
计算机体系概论
“存储程序” 特点?
早期计算机通过硬件开关或打孔纸带输入程序,程序和数据是分离的。老冯提出了把毒和鸡汤存储在一起的思想:把程序和数据存在一起,存在存储器里。
计算机的五个子系统?
我们为什么要造计算机,要算个什么东西。所以输入、输出、算术逻辑运算肯定是有的。怎么算,你在草稿纸上算题,得有你这个人控制,得有中间结果。所以控制和存储是有的。
主机?
主机就是你引脚直接装在主板上的东西,粗略地理解为 CPU + 内存。显示器和鼠标键盘属于输入输出系统,用线连在机箱外面。剩下三个系统就是主机:控制单元和算术逻辑单元 ALU 合称中央处理单元 CPU;存储系统包括硬盘、内存、cache、寄存器,这四个是体积越小、容量越小、价格越贵。但是:硬盘不属于主存,不算在主机里面,它和输入输出系统合称外部设备,即 “用户与计算机通信的界面”。
ALU?
即算术逻辑单元 Arithmetic and Logic Unit
指令和数据?
指令和数据都是二进制的,在形式上无法区分,由控制器判断谁是指令,谁是数据。判断的依据是:当前处于哪个访问阶段,是处于取指周期还是执行周期。当程序被启动执行后,其指令和数据从外存被装进内存。
K?
按具体上下文,单独一个 K 可指 KB,即 2 的 10 次方个字节(Byte)
汇编语言?
汇编语言与具体的机器结构(指令集架构)有关,其源程序不能直接在机器上执行,还得过一道汇编器。
机器语言?
计算机硬件可以直接执行的是机器语言程序,一系列 0 和 1。不是硬件描述语言,硬件描述语言是写电路的,用这种语言描述电路结构。汇编语言还要过一遍汇编器。
机器字长?
机器字长是二进制的位数,是 ALU 和通用寄存器的宽度。指令寄存器和浮点寄存器的宽度可能与其不等。
面向量纲 / 单位计算?
CPI 的单位是:个 (时钟周期) 每个 (指令)
时钟周期的量纲是:时间。这一个时钟周期有它的具体时间长度。
主频的量纲是:频率,时间的倒数。一秒钟被分割成了有多少个时钟周期。
MIPS 的单位是:(百万) 个 (指令) 每个 (秒)
这里的 M 是 10 的 6 次方,主频里的 G 是 10 的 9 次方,往上指数 + 3 为 T P E B
做计算题,先搞明白指令总数、时钟周期总数。指令总数乘上 CPI 等于时钟周期总数。时间就是时钟周期总数乘上每个时钟周期所占的时间长度。
在纸上画图:一个秒被切割成了一系列时钟周期,每个时钟周期执行一条指令。直接设未知数,列方程。
运算方法和运算器
幺二八六四 三二幺六 八四二幺 五二五幺二五 零六二五
在发草稿纸之后,直接把 0 到 F 全写下来(想当年笔者可以把元素周期表画下来(除了镧系和锕系),包括一直到气奥的各个元素名、绝大部分元素符号以及常见的相对原子质量,还有 38324 14122 横批 4546 之类的。但是现在不行了。还有 2^31 - 1 = 2147483647,这是四字节 int 类型的最大值,这个数字最早在《植物大战僵尸》的修改器里见到,如果你无尽模式或者自选关过了这一波,它的程序会崩掉)
原码反码补码移码?
正整数的原码反码补码都是它的二进制按照某一个特定的位数表示,前面补零。
负整数的原码,最高位为符号位 1,后面为它的二进制形式按照某一个特定的位数表示,前面补零。
负整数的反码,为原码除符号位的所有位按位取反后的结果。
负整数的补码,为其反码 + 1,按位截断。
移码 = 【真值 + (最高位所代表的 2 的次方值 - 1)】的无符号整数表示
如八位下 5 的移码是 5 + 2^(8-1) = 5 + 127 =
4 + 128 = 1000 0100
八位下,零的表示形式?
正零的原码:00000000
负零的原码:10000000
正零的反码:00000000
负零的反码:11111111
正零 / 负零的补码:00000000
-26?
26 = 16 + 8 + 2
= 10000 + 1000 + 10
= 00011010
-26 = 10011010(原)= 11100101(反)= 11100110(补)= E6H
BCD 码?
用二进制编码的十进制数 (Binary-Coded Decimal)。对于 8421 码,是把十进制数的每一个位转换成一个四位的二进制数。
如 (1145)_10 = (0001 0001 0100 0101)_BCD
进制转换?
分向十进制转、从十进制向外转、二八十六互转。
向十进制转:各个位的十进制值乘上以原进制为底、该位与小数点的相对位置为指数的幂,再相加。其中小数点左边一位的相对位置为零,小数点右边一位的相对位置为负一,以此类推。
从十进制向外转:除 k 取余法 + 乘 k 取整法。整数部分用短除法列竖式,用新进制的基数去除,除到商为零为止,之前的所有余数从下向上排列为新数的整数部分;小数部分乘上新进制的基数,取积的整数部分为新数的小数部分,积的小数部分继续与基数乘,直到积的小数部分为零或者出现循环节为止。
对于一个 1000 以内的十进制数转成二进制,除 k 取余法还是太教科书了,你可以直接把它拆分成 2 的幂相加,因为加减法不容易出错。
二八十六互转:四位二进制位与一位十六进制位在 [0,16) 这个整数范围内一一对应。小数点前后的部分直接按片段替换。三位二进制位与一位八进制位在 [0,8) 这个整数范围内一一对应。小数点前后的部分直接按片段替换。八与十六互转时,以二作为桥梁。
浮点数的编码方式?
对于 32 位浮点数 float,即单精度浮点数,最高位为符号位,后 8 位为阶码,再后 23 位为尾数。
阶码决定范围,尾数决定精度。
浮点数转真值:把 1. 与 23 位尾数缝合起来,转成十进制;把阶码作为移码求真值,作为 2 的指数;两者相乘,带上符号位。
普通数转浮点数:把绝对值先转成二进制,小数点挪到第一个 1 的后面,为符号 (1.xxx) 乘 2^ 指数;符号放最高位;指数转为移码放后 8 位;小数点后的部分取 “0 舍 1 入” 的 23 位。
(意思就是:1.7 和 -1.7 只差一个符号位)
对于 64 位双精度浮点数 double:阶码变成了 11 位
float 的五种形式?
32 位二进制浮点数,她的位数是有限的,不可能双射无限多(阿列夫一)的(实)数。
- 阶码全零,尾数全零:正 / 负机器零
- 阶码全零,尾数不全零:非规格化数
- 阶码全 1,尾数全零:正 / 负无穷大
- 阶码全 1,尾数不全零:不是数(NaN)
她的阶码有 8 位,当不是全零或全一时,我们称她为规格化的。把阶码移码的身份转回正经数后,指数范围为 [-126,+127],不考虑尾数,对应真值约 2^(-126) 到 2^127,又约 10^(-38) 到 10^38。
浮点数原码运算时,判定结果为规格化数的条件是:尾数的最高位为 1
奇偶校验?
看 1 的个数
串行运算器?
从低位到高位逐位运算
加法器采用先行进位的目的?
加速传递进位信号(没明白)
采用双符号位的定点补码运算器,何时结果溢出?
双符号位不同(没明白)
存储系统
存取周期?
存储器进行连续读和写操作所允许的最短时间间隔(没明白)
存储器采用分级存储的目的?
钱、容量、速度三者不能兼得。
寻址范围?
- 内存能存储多少位二进制数
- 多少位二进制数作为一个地址
- 两者相除,结果无单位
已被淘汰的存储器?
磁芯存储器
主存?
主存由 RAM (Random Access Memory,随机存取存储器) 和 ROM (只读存储器,Read-Only Memory) 组成。同一个存储器里,每个存储单元宽度相同
PROM? EPROM?
前者是可编程 (P) 的 ROM,后者是可擦除的 PROM。
PROM 不一定可被改写。EPROM 可被改写多次,但不能作 RAM
U 盘、TF 卡属于闪存,闪存属于 EPROM
SRAM? DRAM?
一静一动,一快一慢。
前者用于 CPU 缓存。后者用于主存、需要定时刷新、行列地址引脚复用 (RAS 行地址选通信号引脚、CAS 列地址选通信号引脚)
磁盘和磁带?
存取时间与存取单元的物理位置有关。磁带串行存取,磁盘部分串行存取。
存储芯片的地址线数据线?
存储容量 = 地址数 * 位宽
数据线或引脚数目 = 位宽
SRAM 地址线或引脚数目 = log_2 (地址数),与位宽无关
DRAM 地址线或引脚数目 = 0.5log_2 (地址数),与位宽无关
MAR? MDR?
存储器地址寄存器、存储器数据寄存器
MAR 宽度 = log_2 (地址数)
MDR 宽度至少为每次读写操作最多存取的位数
某一 RAM 芯片其容量是 512*8 位,除电源和接地端外该芯片引线的最少数目是多少?
数据线 8 + 地址线 log2 (512)+ 片选线 1 + 读写线 1=19
双端口存储器?
左右端口地址码相同时,发生读写冲突
指令系统
程序控制类指令的功能?
改变程序执行的顺序
RISC?
指令长度固定,减少指令数,增加寄存器数
一地址格式的指令?
一地址格式的算术运算指令,另一个操作数隐含在累加器里
一地址格式的指令,可能有一个操作数,也可能有两个操作数
怎么区分寄存器中的值是地址还是数据?
指令操作码或寻址方式位
一条指令中,操作数的寻址方式?
看指令地址码是什么:
- 操作数所在的存储单元:寄存器间接寻址
- 操作数所在的存储单元地址:直接寻址
- 操作数所在的寄存器编号:寄存器直接寻址
- 操作数本身:立即寻址
CPU 性能指标
\(T\) 时钟周期:计算机中最短的时间。类比:一面有秒针的钟,最短时间为 1 秒。类比:普朗克时间。类比:“一周” 的 “最短时间” 为 “天”
\(f\) 主频 / 时钟频率:一秒钟之内,包含多少个时钟周期。对于一个可以精确到 0.01 秒的秒表,其 “主频” 为 100Hz
\(N_\mathrm{C}\) 时钟周期数:天数、Num of Cycle
\(I_\mathrm{N}\) 指令数:任务数、Instruction Num
\(\mathrm{CPI}\) (Cycle Per Instruction):每条指令平均时钟周期数。完成每个任务的平均天数。你的时钟周期为 “天”,有 100 个任务 (指令) 要完成,完成它们共花了 200 天。你的 CPI 为 2 天 / 任务
\(\mathrm{CPI} \times I_\mathrm{N} = N_\mathrm{C}\)
\(\mathrm{MIPS}\):百万条指令数 / 秒
\(\mathrm{FLOPS}\):浮点操作数 / 秒
\(t_\mathrm{CPU}\) 执行时间:执行一段程序 (若干条指令) 所花费时间。
\[ \begin {aligned} = & 指令数 \times \mathrm {CPI} \times 时钟周期 \\ = & 任务数 \times 每个任务所花天数 \times 一天有多少秒 \\ = & 执行该程序所经过时钟周期数 \times 时钟周期 \\ = & 花了多少天 \times 一天有多少秒 \\ \end {aligned} \]
使用一个字节记录整数
计算机存储的数据由一系列 0 和 1 表示,每个
0 或 1
称为一个二进制位,八个二进制位组成一个字节。一个字节的范围:
0000 0000 - 1111 1111
使用一个字节,可以表示多少种状态?对每一位来说,只有两种可能的状态:0
或 1。一共有八个不同的位,所以可以表示 \(2^8=256\) 种状态。
把 0000 0000 - 1111 1111 转换为十进制数是 \(0\) 到 \(255\),有 \(256\) 个数。它当然可以通过进制转换,表示
\(0\) 到 \(255\) 的整数(也可以叫 “无符号整数”)。
我们想表示负数,可以这样规定:只把后面七个二进制位转换成十进制,而用第一个二进制位表示符号(其中
0 表示正号,1 表示负号),即:
0 0000000 - 0 1111111表示 \(+0\) 到 \(+127\)1 0000000 - 1 1111111表示 \(-0\) 到 \(-127\)
这被称为原码表示法。
我们想用原码计算 \(4 - 7\),即 \(4 + (-7)\):
0000 0100\(-\)0000 0111\(=\)1111 1101,可以看到,结果不是 \(-3\)0000 0100\(+\)1000 0111\(=\)1000 1011,可以看到,结果不是 \(-3\)
因为有符号位干扰,但我们想让符号位也参与计算的同时,加和减的结果相同且满足定义。还是用符号位表示正负,后七个位表示绝对值。
有一台钟(12 个数字的)慢了 3 小时,此时 +3 和
-9 是等价的。它的 “循环周期” 是 12
用后七个位表示绝对值,“循环周期” 就是
128。此时,-7 和 +121 等价
采用补码表示法:
0 0000000 - 0 1111111表示 \(0\) 到 \(127\)1 0000000 - 1 1111111表示 \(-128\) 到 \(-1\)
此时计算 \(4 - 7\):
0000 0100\(-\)0000 0111\(=\)1111 11010000 0100\(+\)1111 1001\(=\)1111 1101
可以看到:
- 正数的补码与原码相同
- 负数的补码:
- 总是以 “全 \(1\)” 来表示 \(-1\),然后依次往前推
- 原码按位取反(除了符号位)后再加一
- 原码从右往左第一个 \(1\) 之前的位(除了符号位)按位取反
普通十进制数转单精度浮点数
交叉引用运算方法和运算器
- 在 IEEE 754 标准下
单精度浮点数,即 32 位二进制浮点数,包含:
一位符号位 + 八位指数位 + 二十三位尾数位
下面的例子中,没有带尾缀的都是十进制,带尾缀 \(\mathrm{B}\) 的是二进制
例一:以 \(0.1\) 为例
把十进制转换为二进制 \(0.1 = 0.0\dot{0}01\dot{1}... \mathrm{B}\)
用以 \(2\) 为基数的科学计数法表示,并保证【尾数的小数点前是 \(1 \mathrm{B}\)】 \(= 1.\dot{1}00\dot{1}...\mathrm{B} \times (2^{-4})\) 可以看到指数是 \(-4\)
计算指数位(又叫阶码),用指数加上偏移量 \((2^{e-1}-1)\)
这里 \(e\) 等于【用于表示指数位的位数】 \(8\),所以偏移量为 \(127\)
则阶码为 \(-4 + 127 = 123\)
阶码的二进制为
0111 1011,注意 阶码为无符号整数取科学计数法的【小数点后二十三位】作为【尾数位】,因为是无限的,所以要舍去一部分
它的前二十位是:
1001 1001 1001 1001 1001二十一至二十八位是:
1001 1001所以二十一至二十三位,要么取
100,要么取101。第二十四位是
1,0 舍 1 入,所以取101把符号位连同阶码、尾数位缝合起来
0 | 0111 1011 | 1001 1001 1001 1001 1001 101
例二:以 \(-12 = 1.5 \times (2^{3})\) 为例:
把十进制转换为二进制
\(12 = 1100 \mathrm{B}\)
用以 \(2\) 为基数的科学计数法表示,并保证【尾数的小数点前是 \(1\)】
\(= 1.1\mathrm{B} \times (2^3)\)
可以看到指数是 \(3\)
计算指数位(又叫阶码),用指数加上偏移量 \((2^{e-1}-1)\)
这里 \(e\) 等于【用于表示指数位的位数】 \(8\),所以偏移量为 \(127\)
则阶码为 \(3 + 127 = 130\)
阶码的二进制为
1000 0010,注意 阶码为无符号整数取科学计数法的【小数点后二十三位】作为【尾数位】,因为是有限的,所以后面直接补零
小数点后二十三位是:
1000 0000 0000 0000 000把符号位连同阶码、尾数位缝合起来
1 | 1000 0010 | 1000 0000 0000 0000 000
如何验证:
- 在线转换
- Wikipedia | 维基百科
- 获取国际标准文件。IEEE 754 标准是电气与电子工程师协会(Institute of
Electrical and Electronics
Engineers)制定的关于浮点数表示和运算的标准。最新标准是 IEEE
754-2019,对应国际标准 ISO/IEC
60559:2020,预计下一次在 2028 年修订。http://snti.ru/
这个网站分享了各种国际标准文件的磁力链接,但是可以免费下载的不全,IEC
的只有 61xxx。据说可以给站长发邮件要
popov_al@perm.ru,每个文件一刀乐。在 ISO 官网上下载需要 187 瑞士法郎,合 1000 多人民币。
用 GDB:
1 |
|
在第六行打上断点,VSCode 开调试,在调试控制台里:
1 | -exec x/4tb &num |
-exec执行命令x查看内存4输出 4 个单元- 不写默认为
1
- 不写默认为
t以二进制形式输出x十六进制
b以【一个字节】为一个单元h两个字节w四个字节g八个字节
&取变量地址
输出结果:
0x61fe1c: 10011010 10011001 11011001 00111111
从右往左排列后:
00111111 11011001 10011001 10011010
0 01111111 10110011001100110011010
才是 float 1.7 的二进制表示。
还可以直接用
1 | -exec x/tw &num |
输出四个字节,结果:
0x61fe1c: 00111111110110011001100110011010
Vue 实现点击 Echarts 图表的一部分后更新另一个图表
环境:
1 | { |
组合式 API。一个 View 的父组件里面有两个 Echarts 图表的子组件 A 和 B。
问题:图表的数据从何而来:
- 在清洗和导出数据的时候直接导出为 Echarts 所需要的 JSON 格式的文件
- 准备图表的 option 的 JSON 格式为一个计算属性,把 data 字段设置为 Ref 对象的 value
- 给 v-chart 标签的 :option 绑定这个计算属性
- 写一个更新图表的函数,fetch 一个文件,转换成图表需要的格式,赋值给那个 Ref.value
点击子组件图表后的事件和参数如何传递给父组件:
- 在子组件里定义一个发射源 const emit = defineEmits (["eventName"]);
- 给子组件 v-chart 标签的 @click 绑定一个方法
- 该方法带一个参数 param 为图表点击后的参数,在该方法里发射事件 emit ("eventName", param);
- 在父组件里引用子组件标签处的 @event-name 绑定一个带参数 param 的方法,用于接收子组件发射的事件和参数
父组件如何向子组件传消息:
- 在子组件里定义它的属性
1 | const props = defineProps({ |
- 在父组件里引用子组件标签处的 :prop-name 绑定一个 Ref 对象,更新 Ref 对象
如何实现点击图表 A 的一部分后,更新图表 B:
- 把点击图表 A 后的事件和参数 emit 给父组件
- 父组件在 A 组件标签 @ 处绑定的方法处接收,并更新图表 B 标签的 :prop-name 的 Ref
- 在 B 组件里监视它 props 的变化,调用更新图表的方法
1 | watch( |
- 在更新图表的方法里,根据接收到的参数,fetch 不同的文件,赋给 data 的 Ref.value
Word 文档模板留存
- 对称页边距,留出一点装订距离。上下 2.5 cm,内 3 cm,外 2.5 cm
- 第一面是封面,第二面是目录。页码从第三面开始编 1,奇数页在右下角,偶数页在左下角
- 所有中英文标题都是黑体加粗,格式都是
1.1.标题。一级标题三号,二级标题四号,三级标题小四。不缩进 - 所有正文中文都是宋体,西文都是 Times New Roman。字号都是小四。首行缩进两字符,左对齐
- 所有标题和正文段落都是段前段后 0,行距 1.5 倍
- 大部分代码用截图,把 VSCode 的背景调到纯白
- 把 VSCode 编辑器的字体调为中文宋体,西文 Consolas
- 单独定义一个图片样式,应用于段落的阴影边框,宽度 0.75 磅
- 小部分短的代码(Shell 命令之类的)单独定义一个代码样式继承自正文,使用与图片同款的边框,首行缩进 2 字符
- 参考文献样式继承自 “列表段落”,悬挂缩进 2 字符,左对齐,允许西文在单词中间换行
解决 VSCode 集成终端按键与快捷键冲突
Ctrl + Shift + P
打开命令面板,搜键盘快捷方式,搜冲突的按键,右键更改 When 表达式,加上
&& !terminalFocus
用 browser-sync 实现在文件内容改变后立即刷新页面
起因是:不管是直接打开 html
文件,还是用 python -m http.server 8000 --bind 127.0.0.1,在修改保存
html 文件后浏览器都不能立马刷新。
1 | npm install browser-sync |
1 | npx browser-sync start --server --files "." |
--files 后指定要监视的文件。
. 表示监视当前目录以及子目录下的所有文件。
可以改成 *.html,public/*.* 等。
html
文件里至少得有一对 <body> 标签,要么没法自动刷新。
Python
Anaconda
不要把包都安到 base 环境里。
1 | conda env export > environment.yml # 导出当前环境依赖 |
报菜名
Python 的标准库有上百个。用 import 还是
from ... import ...,后面加不加 as
,以易读为主。因为代码是给人看的。
使用 from xxx import *
类似于:你在搭积木的时候,闭着眼睛把一整个塑料袋的积木全倒出来,然后闭着眼睛摸一个、闭着眼睛摸一个。
import 语句的顺序是:标准库、第三方库、自定义库。可通过
VSCode 插件 isort 解决,按 Ctrl + Shift + O 排序。
在你的工程目录下面,使用 https://github.com/bndr/pipreqs
可以把你用到的所有第三方库写到依赖文件 requirements.txt
里。
虽然 Python
的一个变量名可以赋多个类型,但在有必要的情况下,还是加上类型注解。这对
VSCode
的代码补全也有帮助:把鼠标移到一个变量名上边,如果你想要它是某一个类的对象,但是它显示为
Any,这时候你在它后面加 .,VSCode
没法给你列出它的方法。这时候你需要显式标注它的类型,比如
foo: Bar。或者 assert isinstance(foo, Bar)
输出函数名和本地时间
使用装饰器:
1 | import datetime |
上面是一种很笨的方法,我们可以用其自带的 logging 模块记录日志到文件:
1 | import datetime |
日志有五个等级:DEBUG 调试诊断用的;INFO 确认正常运行;WARNING 是不影响正常运行的错误,如向数据库里插入一条已经存在的记录,然后忽略它;ERROR 是影响正常运行的错误,如数据库连接失败(但是你系统的其他功能可用);CRITICAL 是你的系统的关键功能不可用(如果你的系统必须要用数据库)。
plt
条形图和柱形图的区别是:前者是横着的,后者是竖着的。前者用
plt.barh,后者用 plt.bar
中文字体:
1 | plt.rcParams["font.family"] = "SimHei" |
最小二乘法多项式拟合
1 | import numpy as np |
scipy.stats. 某种分布.
\[ \begin {aligned} \mathrm {rvs (分布参数,size = 实验次数)} & = X\\ 离散型 \mathrm {pmf}(分布参数,k = [x_1,x_2, ...]) & = \mathrm {P}(X = x) \\ 连续型 \mathrm {pdf}(分布参数,x = [x_1,x_2, ...]) & = f_{X}(x) \\ 离散型 \mathrm {cdf}(分布参数,k = [x_1,x_2, ...]) & = F_{X}(x) = \mathrm {P}(X \le x) \\ 连续型 \mathrm {cdf}(分布参数,x = [x_1,x_2, ...]) & = F_{X}(x) = \mathrm {P}(X \le x) \\ 返回 \mathrm {numpy.ndarray} \end {aligned} \]
selenium
1 | import json |
Java
Maven 仓库 | 阿里云 Maven 仓库 | Spring Boot 文档 | Spring Boot 支持的 Java 版本
关键字:没有 unsigned 关键字
运算符:无符号右移 >>>,前面直接补零。
- C/C++/Java 在对整型变量右移
>>时:- 正整数前面全补
0 - 负整数前面全补
1 - 无符号整数前面全补
0 - 作用相当于除以 2
- 正整数前面全补
数据类型:布尔 boolean,值为 true 或者
false。可以直接用,占一个字节。
- 写
if(3 == true)时会报错,数据类型不同,不能直接比较。 - 在 C 的
<stdbool.h>中被#define了为1和0。- 写
if(3 == true)时会跳过分支。
- 写
- C++ 同 C,但是不用引头文件,可以直接用。
- 在 Python 中是首字母大写的,也相当于
0和1,但是数据类型不同。- 写
if(3 == True)时会按1比较。 - 写
if(3 is True)时会报错。
- 写
- 在 JS 中也相当于
0和1,但是数据类型不同。- 写
if(1 == true)时会执行分支。 - 写
if(1 === true)时会跳过分支。
- 写
字符 char:无符号的两个字节。在 C/C++ 里是一个字节。
有符号整型
byte:一个字节short:两个字节int:四个字节long:八个字节
语法:
1 | Type[] arr = ... |
接口:接口是一种特殊的类。写出来就是用来被继承的 —— 不用
extends(扩展),用 implements(实现)。
1 | public interface USB { |
一个类只能 extends 自一个父类,但可以
implements
多个接口。实现接口的子类必须得实现接口里声明的方法。
JavaBean 规则:
- 必须有一个无参构造方法
- 所有属性私有,且对其提供 public 的
getXxx()与setXxx()方法
JSP
Web 是一种分布式的应用框架。基于 Web 的应用是典型的浏览器 / 服务器(B/S)架构。——ISBN 9787302438090
JSP 技术是以 Java 语言作为脚本语言的,JSP 网页为整个服务器端的 Java 库单元提供了一个接口来服务于 HTTP 的应用程序。—— 菜鸟教程
笔者测试,用 VSCode 和 IDEA 社区版(2024.1)都没办法格式化 JSP 代码,或者是暂时没找到解决方法。或者你可以用 CSDN 网友分享的 IDEA 破解版(不是用蓝绿修改器破解的) https://blog.csdn.net/hlizoo/article/details/137562771
用 VSCode 或 IDEA 社区版
1 | mvn archetype:generate "-DgroupId=com.example" "-DartifactId=demo" "-DarchetypeArtifactId=maven-archetype-webapp" "-DinteractiveMode=true" |
VSCode 使用 Community Server Connectors 插件、IDEA 使用 Smart Tomcat 插件
用 Eclipse 2020-03 (4.15.0)
在首选项里设置 JDK 和 Tomcat 的路径。
New -> Dynamic Web Project
按 Ctrl + Shift + F 格式化代码 —— 這個快捷鍵會和 Win10 的微軟拼音輸入法簡繁體切換功能衝突。解决方法除了再按一次,还可以右击你任务栏上的 [中],进输入法设置,把热键关了。
一个 JSP 文件的示例
1 | <%@ page language="java" contentType="text/html; charset=UTF-8" |
它在 html 的基础上扩展了一些标签。可以使用 Java 库。
JSP 运行的原理
- 客户向 Tomcat 服务器发送 HTTP 请求
你可以使用 Fiddler
来抓包(或者直接用浏览器控制台抓,这是最方便的)。在 Eclipse
里按 “播放键” 之后,Eclipse 向 localhost:8080 发送了一个 GET
请求。
使用
1 | netstat -ano | grep 8080 |
查与 8080 端口有关的进程号。再打开任务管理器的详细信息,查到进程为
javaw.exe。右击打开文件所在位置,在你 Eclipse
首选项里设置的 JDK 目录的 bin 目录里面。
使用
1 | jcmd |
查看 java 进程,为
org.apache.catalina.startup.Bootstrap start
- Tomcat 启动一个线程,把 jsp 文件转换成 java 文件
(一个继承自 javax.servlet.http.HttpServlet
的类,头上带一个注解 @WebServlet("/path"),相当于 Python 的
Flask 框架里的 @app.route("/path"))
- 把 java 文件编译成 class 文件(字节码)
jsp 指令与 jsp 动作?
前者是静态的,后者是动态的(感性认识)
前者类似
1 | <%@ include file = "sub.jsp" %> |
后者类似
1 | <jsp:include page = "sub.jsp"/> |
在一个 jsp 页里,如何把表单传递给另一个 jsp 页?另一个 jsp 页如何接收?
三种方式:(使用 get 方法会在 url 里看到请求参数,post 不会)
- 【包含对面的】
jsp:include配合jsp:param。这是把另一个 jsp 页包含进来。
1 | <form method="get"> |
- 【请求转发】先使用本页面的 Java 代码处理表单,再使用
jsp:forward配合jsp:param,把 request 对象转发给另一个 jsp 页面。
这种把 JSP 标签和 Java 代码混在一起的写法很新鲜:
接收方用 request.getParameter("name") 接收
1 | <form method="post" action=""> |
- 【重定向】
response.sendRedirect("result.jsp")不会把 request 对象传递过去
应 session.setAttribute("name", value)
对方使用 session.getAttribute("name") 接收。
访问使用 response.sendRedirect 的一方 jsp 时,会跳转到对面的一方
重定向和请求转发
重定向会丢失 request 对象,请求转发不会。
在 JSP 或者 Servert 里请求转发:
1 | request.setAttribute("studentList", studentList); |
如何实现点一个按钮出现一个新表单?
在第一个表单里加一个隐藏的 <input>
标签,第一个表单提交给本页面,然后在本页面里写 Java 代码:
笔者觉得这比 JS 操作 DOM 看起来新鲜,很好玩。
1 | <form action=""> |
Filter 是什么?
一个实现了 javax.servlet.Filter 接口的类。可在
doFilter 方法里对请求预处理,响应后处理:
1 |
|
如何使用 JDBC 连接 MySQL
- 下载驱动 Jar 包 https://dev.mysql.com/downloads/connector/j/
- 把 Jar 包 复制到
yourprojectname\WebContent\WEB-INF\lib
插入的问题
MySQL 里有两张表,一张表的外键是另一张表的主键(如 id),级联更新和删除。如何插入 “一条” id 的记录 “分散给” 这两张表?即对这两张表分别插了一个 id 相同的记录。
先插 id 为主键所在的表,后插 id 为外键所在的表。
这是关系型数据库原理的知识。本表里的 “外键” 就是引用外部表里的 “主键”,那得先有外部表。
乱码的问题
保证这些地方的编码是 UTF-8:
- Eclipse 首选项里的文件编码
- 搞一个 Filter
- MySQL 数据库表的编码
1 | <%@ page language="java" contentType="text/html; charset=UTF-8" |
排序算法
二分查找就是翻书。有一本 200 页的书,你想翻到 124 页,一下就翻到的概率是很小的。翻到中间,发现是 100 页;翻到 100~200 页的中间,发现是 150 页;翻到 100~150 页的中间,发现是 125 页,以此类推。
二分查找就是从列表里查找一个值,前提列表是有序的,这样可以比较大小,在二分之后仍然是有序的。如果要查找的值比列表的中间值小,就在列表的左半部分找,这就是二分。这时需要变换查找范围的右边界,到中间值的左边一个位置。然后对查找范围继续二分,与中间值作比较,如果要查找的值比中间值大,就在查找范围的右半部分找,这时需要变换查找范围的左边界到中间值的右一个位置。以此类推,如果找到了,就返回目标元素的索引。找不到就返回 - 1。
插入排序:一张一张地接扑克牌,接到第一张扑克牌时什么也不做,接到第二张扑克牌时要与第一张作比较,看插入到第一张的前面还是后面,……,接到第 n 张扑克牌时要与前 n - 1 张比较,看插入到手牌的哪个位置。
选择排序:拿到一手混乱的牌,从中选取最小的,与第 0 张交换位置;之后忽略第 0 张,从剩余的牌里选取最小的,与第 1 张交换位置;之后忽略第 0、1 张,从剩余的牌里选取最小的,与第 2 张交换位置。以此类推。
归并排序:把一沓牌分成一张一张的,摆在桌子上。相邻的两张合并成一个组;相邻的两组分别排序,合并成一个新组;以此类推。
快速排序:选一个基准,所有比基准小的放在基准左边,比基准大的放在基准右边。然后就分成了两个区,对每一个区里的元素再选一个基准,重复上面的操作。
数据挖掘
属性与度量
- 测量:将对象的属性映射为数值 / 符号值
- 测量标度:函数、秤
例如:秤将人的体重映射为一个数值
属性的类型(也叫测量标度的类型):
分类的(定性的)
- 标称:有意义的只有等于 / 不等于操作。例如你的性别,不能与其他性别进行比较大小、加减、乘除操作
- 序数:有意义的有:等于 / 不等于和比较大小。例如你的成绩在这五个档次里面 {A,B,C,D,E}
数值的(定量的)
- 区间:除了能等于 / 不等于 / 比较大小,还要能加减。比如某年某月某日、华氏 / 摄氏温度
- 比率:在上面的基础上,还要能乘除
离散的属性:可取有限个值,或无限可数个值
连续的属性:取实数值
非对称的属性:出现非零值比零值重要
关联分析
1 | class AssociationRule(namedtuple("AssociationRule", ["X", "Y"])): |
支持度计数 sigma,即事务列表里,项集的超集个数
支持度,即项集的超集个数与集合总个数(事务个数)的比值
大于等于最小支持度(计数)的项集,称为频繁项集
置信度,由 X 引起 Y 的可能性。X 的支持度计数做分母,XY 并集的支持度计数做分子
先验原理:如果一个项集是频繁的,它的所有子集都是频繁的
反过来:如果一个项集是非频繁的,它的所有超集都是非频繁的
即:一个项集的子集的支持度,大于等于它本身的支持度
针对购物篮数据集的关联分析
关联分析到底是什么意思?是发现隐藏在大型数据集中的有意义的联系。
购物篮数据集怎么表示?是一张表,表里有一系列行,每一个行是一个事务,每一个事务表现为一个集合,这个集合里有一系列商品的名字,比如 {"面包","牛奶","尿布"}
联系怎么表示?有两种形式:关联规则、和频繁项集
关联规则是什么意思?是两个不相交集合的蕴含表达式,如 {尿布}->{啤酒} 这个表达式的意思是:购买尿布,引起了购买啤酒,前面是因、后面是果。
项集是什么意思?是一些项的集合。是
list[str]
什么叫频繁项集?是支持度或者支持度计数大于等于最小阈值的项集。
什么叫支持度计数?是该项集在事务列表里的超集数量,是事务列表里的所有包含该项集的事务数量。
什么叫支持度?是事务列表里,包含该项集的事务的数量占所有事务数量里的比值。
{面包,牛奶} 支持度 0.3 是什么意思?是在所有的购物记录里,同时包含购买了面包、牛奶的购物记录的比值。是在每 10 次购物里,就有三次同时购买了面包和啤酒。
怎么挖掘关联规则?分两步:
- 产生频繁项集: 发现满足最小支持度阈值的所有项集
- 什么意思?项集里有几个元素?最少有一个,最多有
len(unique(flatten(basket)))个,是所有独立的商品组成的集合。
- 什么意思?项集里有几个元素?最少有一个,最多有
- 产生规则
- 提取所有高置信度的规则。
格结构是什么意思?格结构里的所有节点构成一个集合的幂集。格结构的第一层是
null,第二层是所有 1 - 项集,第三层是所有 2 - 项集…… 最底层是
len(unique(flatten(basket))) 项集
先验原理是什么意思?如果一个项集是频繁的,它的所有子集都一定是频繁的。
什么叫一个项集是频繁的?它的支持度计数大于等于最小阈值
什么叫一个项集的子集是频繁的?它的子集的支持度计数大于等于最小阈值
为什么项集支持度计数大于等于最小阈值后,它的所有子集的支持度计数都会大于等于最小阈值?
支持度计数 +1 的操作是在什么时候?把这个项集和事务列表里的所有项集做比较,如果该项集是事务列表里项集的子集,把该项集的支持度计数 +1。所以:支持度计数,就是找超集数量
一个集合的子集的超集数量,必定大于等于该集合的超集数量,为什么?因为这个集合本身就是它子集的超集。
什么叫基于支持度的剪枝?把先验原理反过来说:如果一个项集是非频繁的,它的所有超集都是非频繁的。
非频繁是什么意思?支持度计数小于最小阈值,超集数量小于最小阈值,包含它的事务数量小于最小阈值
如果一个集合的超集数量小于最小阈值,它的(所有超集)的超集数量都会小于最小阈值。为什么?你确定这句话对吗?
正确的描述方法是:如果包含 A 的事务数小于最小阈值, 那么包含(A 的超集)的事务数会小于最小阈值。为什么?
因为在一个购物篮里,事务数量是有限的。
支持度计数 +1 的操作是在什么时候?是针对一个项集,判断各个事务是不是它的超集的时候。
1 | basket = [ |
问:[2,3] 的支持度计数是几?是 2,是第一行和第四行
现在规定:最小支持度计数是 3。问,[2,3] 超集的支持度计数?既然是超集,考虑它自己是它自己的超集这种情况,它的支持度计数还是小于 3。现在再往里加一个,能达到要求吗?加一个之后,超集的判定变严了。
理性的说法是:原来是 A 超集的集合 B,在 A 加一个元素之后变成 C 后,B 不一定还是 C 的超集,因为新加的那个元素可能不在 B 里。如果新加的那个元素在 B 里,C 超集的数量(相对于购物篮)至少减零。如果不在 B 里,C 超集的数量(相对于购物篮)至少减一。
基于支持度的剪枝什么意思?如果一个项集是非频繁的,把它格结构里所有的超集剪了。
反单调性什么意思?一个项集的支持度小于等于它的自己的支持度。
numpy 库的多维数组切片语法
1 | import numpy as np |
1 | import numpy as np |
Apriori 算法
%%{
init: {
"theme": "neutral",
"fontFamily": "Times New Roman"
}
}%%
flowchart TD
A[产生频繁1-项集] --> B[k=1] --> C[k+=1] --> G[由频繁k-1-项集生成候选k-项集,并剪枝] --> D{候选k-项集为空?}
D -- 是 --> E[返回频繁项集]
D -- 否 --> F[对候选k-项集支持度计数,产生频繁k-项集] --> GG{频繁k-项集为空?} -- 是 --> E
GG -- 否 --> C
直接看 mlxtend 库的源码(删除了一些相对于算法本身无关紧要的,比如低内存下的算法和 pandas 兼容性的问题):
1 | from itertools import combinations |
鸢尾花数据集关联分析示例
1 | import os |
动态规划
滚动数组怎么滚
以三个数为例:
- 先处理前两个,直接返回
- 声明三个变量,只给前两个赋值
- 循环 [下标看具体情况] 在每次循环里:
- 先作用
- 把第二个数赋值给第一个
- 把第三个数赋值给第二个
- 返回第三个
笔者认为这种写法符合人的直觉,且不容易出错。
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
换一种问题描述方式:把一个正整数 n 拆分成一系列 1 和 2 有顺序地相加,共有几种拆分方式 f (n)?
从它的尾巴向前看,有这两种:
- n = (n-1) + 1
- n = (n-2) + 2
其中 (n-1) 和 (n-2) 有它们各自被拆分的种类数,于是 f (n)=f (n-1)+f (n-2)
边界:f (1)=1,f (2)=2(2=1+1=2+0)
1 | int climbStairs(int n) { |
746. 使用最小花费爬楼梯
我们把问题描述改写一下:
给你一个非负整数数组,长度大于等于 2,让你在数组里选一些数求和,要求选的这些数:
- 0 号和 1 号元素必须二选其一
- 最后两个元素必须二选其一
- 选的相邻两数之间至多间隔一个数
- 要求和最小,输出和
状态转移就是从过去转移到现在。现在虚空设一个数叫 dp [i] 表示爬到下标为 i 的台阶时的花费
(注意:此时的 dp [i] 是不包含本级台阶的花费的,往后跨了之后才加)
有两种转移的情况:从 i-1 爬一层、从 i-2 爬两层
从 i-1 爬一层之后、转移到现在,现在的花费等于跨上一步之前的花费 + 跨上一步之后的花费
即 dp [i] = dp [i-1] + cost [i-1]
总的状态转移方程为 dp [i] = min (dp [i-1] + cost [i-1], dp [i-2] + cost [i-2])
边界为 dp [0]=dp [1]=0,返回值为 dp [n],下标 n 在楼梯的顶层,cost 数组右边一个位置,等于 cost 数组长。用滚动数组,循环 [2, cost 长]
1 | int minCostClimbingStairs(int* cost, int costSize) { |
198. 打家劫舍
我们把问题描述改写一下:
给你一个长度 [1,100] 的非负整数数组,让你选一些数求和,要求选的这些数间隔至少为 1,返回最大和
虚空设一个数 dp [i] 表示你对 i 号下标纠结之后的和,你正在纠结打还是不打
- 如果打 i,就不能打 i-1,dp [i] = dp [i-2] + value [i]
- 如果不打 i,就可以打 i-1,dp [i] = dp [i-1]
这两种情况求大的
1 | int rob(int* nums, int numsSize) { |
用 C 语言模拟一个像素时钟
myclock.h
1 |
|
myclock.c
1 |
|
Hadoop
一种不看完整教程安装软件的方法:
- 在软件安装的目录里面,通常有一个 doc 文件夹
- 在解压软件包之后,什么配置都别写,上来先启动了再说
- 找到软件的日志文件在哪里
- 在日志里搜索
WARNERROR - 在网上搜索或者问 AI 为什么会出现这个错误
VSCode 远程附加调试
hadoop-env.sh
1 | export 某某_OPTS="-agentlib:jdwp=transport=dt_socket,address=8888,server=y,suspend=n" |
launch.json
1 | { |
Java 代码运行环境的问题
“连接
HDFS” 是什么意思?再往前问:你是如何知道你的 “集群” 是正在运行着的?用
jps 查看 Java 进程。
jps 查看的是什么?是所有正在运行着的 JVM
实例,每一个进程是一个单独的 JVM。
“连接 HDFS” 的意思是:再运行一个新的 JVM,称为 “客户端”。这个 JVM 要与另一个 JVM 通信,那个 JVM 叫 NameNode。怎么通信?虽然不知道细节,但你可能看过这样的代码:
1 | package com.example; |
现在的问题在于:
- 它
import的东西是怎么来的? - 在它编译完之后,放到 JVM
上运行的时候(即 “运行时”),它还需不需要它
import的东西? - 它运行时的 JVM 在哪里,在虚拟机上还是在物理机上?如果在物理机上,它能不能与虚拟机通信?
- IDE 起的是什么作用?
先回答第四个问题:IDE 起的是工具人的作用。如果你用的 IDEA,并且成功连接 HDFS 了,你会在 IDEA 的命令行看到:
1 | /lib/jvm/java-8-openjdk-amd64/bin/java -javaagent:/opt/idea-IC-241.15989.150/lib/idea_rt.jar=43273:/opt/idea-IC-241.15989.150/bin\ |
它就是执行了一条命令:打开你的 JDK 目录里的 java
,然后向这个东西传了几个参数:工具人、文件编码、classpath
关键的就是 classpath,你需要保证你代码 “运行时” 的东西能在 classpath 里找到。
再回答第二个问题:它 import
的东西都是它的 “运行时” 需要的东西吗?
不一定,这是它 “编译时” 需要的东西。当他报错报找不到某个类的时候,就是它 “运行时” 需要的东西。
再回答第一个问题:搞到这些 jar 包。
- 用 Maven
- 如果你看过你 Hadoop 的安装目录,你会看到一个
share文件夹
对于第三个问题的解决思路:
- 在虚拟机上运行客户端,连接虚拟机上的 NameNode
- 在物理机上运行客户端,连接物理机上的 NameNode(如果你物理机搞成功了)
- 在物理机上运行客户端,通过 winutils 这个中间人与虚拟机上的 NameNode 通信
笔者最终的解决方案是:在虚拟机上安装 IDE,把
$HADOOP_HOME/share/hadoop 里的 Jar 包导进 IDE
里(这里用的是 IDEA),按播放键运行。如果报找不到类的错误,注意:在
$HADOOP_HOME/share/hadoop/子文件夹 下还有一个叫
lib 的文件夹。
安装 Ubuntu 22.04.3
- 下载 Linux 操作系统镜像,可以理解为操作系统的 “安装包”。https://launchpad.net/ubuntu/+cdmirrors
- 下载一个支持在 Windows 操作系统下运行 Linux
镜像的软件(宿主),它相当于一个没装操作系统的电脑,但是装了引导加载程序
GRUB
- 使用 VM Player
- 在宿主里 “创建两台虚拟机”,相当于对这一份镜像,安装了两个新的操作系统,运行在你的宿主和 Windows 操作系统上
前面三步改用 WSL(适用于 Linux 的 Windows 子系统)https://learn.microsoft.com/zh-cn/windows/wsl/
配置网络,给虚拟机和物理机搭上鹊桥
- 不同虚拟机采用不同静态 IP
- 把虚拟机网卡路由到宿主的网关,在
C:\ProgramData\VMware\vmnetnat.conf查看 VM 的 NAT 网关地址 - 修改
/etc/hostname为自定义主机名 /etc/hostsC:\Windows\System32\drivers\etc\hosts
如果你用的是 WSL,你在它上面开一个端口,可以直接在物理机上使用
localhost:port 访问。如果你装了两台 WSL,它们的 IP
会是相同的,这个问题不好解决。据说学大数据的都找不到大数据相关工作。那我们就退而求其次,根本没有必要搭分布式集群,在一台机器上搭个伪分布式就行了,文件分片只分一片。这样配置文件还不至于备份来备份去,只保留一份配置文件。
配置 Ubuntu 软件源 https://mirrors.ustc.edu.cn/help/ubuntu.html
安装 JDK https://cwiki.apache.org/confluence/display/HADOOP/Hadoop+Java+Versions
写环境变量
配置 SSH https://wangdoc.com/ssh/
网络
如果你用的 WSL + 单机伪分布式,只需要修改
/etc/wsl.conf:
1 | [network] |
1 | exit |
如果你用的 VM + Ubuntu 22.04:
编辑 /etc/netplan 下的 00-installer-config.yaml 文件。netplan
文档
选择 192.168.78 的依据是:
- 在物理机使用
ipconfig命令得到的【VMnet8】的 IPv4 地址192.168.78.1 - 查看
C:\ProgramData\VMware\vmnetnat.conf里的 NAT 网关地址192.168.78.2
1 | network: |
1 | sudo netplan try |
SSH
如果你用的 WSL + 单机伪分布式,下面两条命令只用做一次。
如果你搭的分布式:每台机器上都执行:
1 | ssh-keygen -t rsa -m PEM |
笔者这里的版本是
OpenSSH_8.9p1 Ubuntu-3ubuntu0.6, OpenSSL 3.0.2 15 Mar 2022,要加上
-m PEM,确保私钥以 -----BEGIN RSA PRIVATE
KEY----- 开头。后续错误
每台机器上都执行:
1 | ssh-copy-id ubuntu101 |
存储空间
1 | sudo du -h --max-depth=1 |
- 给虚拟机扩容:
https://hrfis.me/blog/linux.html#扩容 - 使用 https://www.diskgenius.cn/ 可以把你 D 盘的空间向 C 盘匀一点。如果你有多余的恢复分区,可以把它删了,只保留一个。
- 使用 https://github.com/redtrillix/SpaceSniffer 可以可视化地展示你硬盘的占用情况。
中文字体
1 | sudo apt install language-pack-zh-hans |
1 | LANG=zh_CN.UTF-8 |
Hadoop 3.3.6
- 下载 Hadoop 软件包
- 在虚拟机上直接用
wget - 用物理机下载它,从物理机的文件系统上再转移到虚拟机的文件系统上(在你的物理机硬盘上表现为
.vmdk文件)- VM Player
有共享文件夹功能,把你物理机硬盘的某一个文件夹挂载到虚拟机的
/mnt/hgfs/Shared - 如果使用 WSL,你的物理机硬盘会被挂载到虚拟机的
/mnt - 使用 XFtp 软件,与你的虚拟机进行 SSH 网络协议连接
- VM Player
有共享文件夹功能,把你物理机硬盘的某一个文件夹挂载到虚拟机的
- 在虚拟机上直接用
- 在两台虚拟机上都把软件包解压。
/opt目录是空的,option 的意思,让你自己选择装不装到这里。
配置
- 修改它们的配置文件,要保证每台机器配置文件内容相同。使用 VSCode 的 Remote-SSH 插件可以直接修改虚拟机内的文件,如果你用的是 WSL 更方便。
在 $HADOOP_HOME/share/doc/hadoop/index.html 左下角有默认的配置文件。
hadoop-env.sh指定 JAVA_HOME,启动 JVM 时的参数core-site.xml指定 hdfs 的 URI,文件系统存在本地哪个目录hdfs-site.xml指定谁当 NN、2NN,副本个数mapred-site.xml指定 MR 框架,MR 历史服务器yarn-site.xml指定 RM,YARN 历史服务器workers指定谁当 DataNode
勤看日志。当 CPU 占用高,写磁盘不到 1MB/s,可能是出问题了在一直写 log。
- 我们为什么要在
hadoop-env.sh里写JAVA_HOME?因为没写的时候,它会报错: JAVA_HOME is not set and could not be found; - 我们为什么要配置 SSH?因为没配置它会报错:Could not resolve hostname xxx: Name or service not known;
- 我们为什么要在
core-site.xml里配置fs.defaultFS?因为没配置它会报错:Cannot set priority of namenode process xxx。在日志文件里有:No services to connect, missing NameNode address; - 我们为什么要在
core-site.xml里配置hadoop.tmp.dir?因为它默认存在/tmp文件夹下,而/tmp文件夹一重启就没了; - 我们为什么要在
hdfs-site.xml里配置dfs.namenode.http-address?因为我们想用浏览器访问 HDFS; - 我们为什么要在
core-site.xml里配置hadoop.http.staticuser.user?因为如果不配置,只有读的权限,没有写的权限; 我们为什么可以不在hadoop-env.sh里配置各种用户名?因为还没有遇到报错的时候
- 在 NameNode 上执行
hdfs -namenode format,把 Hadoop 的文件系统 HDFS 初始化。在你的物理机文件系统上有一个虚拟机文件系统,在虚拟机文件系统上又有一个 HDFS
MapReduce 编程入门
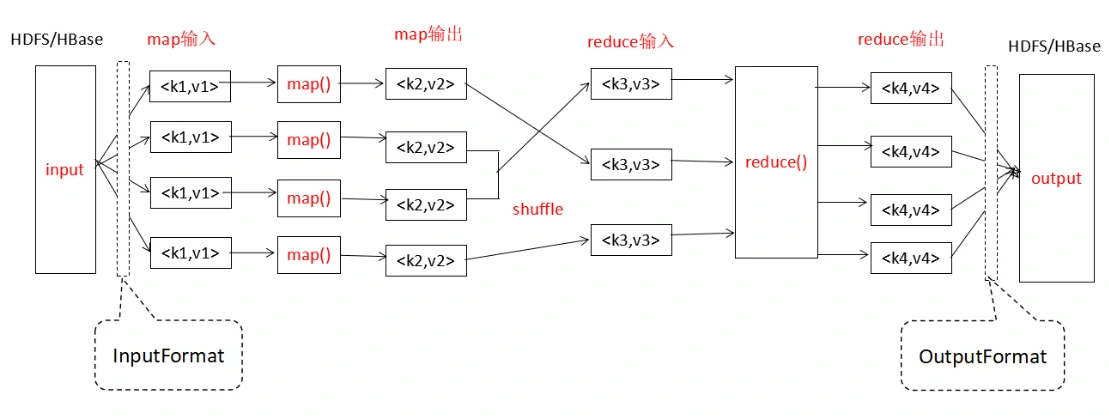
我们想统计一篇英文文章里的单词,每个都出现了多少次。假设这个文本文件只有英文单词、空格和换行符(LF 或者 CRLF)。
需要继承 Mapper 类,重写它的 map ()
方法。这个方法里传了三个参数:该行的偏移量、该行的文本内容、环境上下文。在这个方法里,对每一行按空格进行分割,形成一个
String [],遍历这个 String [],把它写到上下文里,这样写的就是一系列
<word,1>。
1 | public class WordCountMapper extends Mapper<LongWritable, Text, Text, IntWritable> { |
继承 Reducer 类,重写 reduce () 方法。
1 | public class WordCountReducer extends Reducer<Text, IntWritable, Text, IntWritable> { |
继承 Driver 类,进行一些配置。
1 | public class WordCountDriver { |
FileAlreadyExistsException:不要提前建好输出文件夹
HDFS
1 | start-dfs.sh |
1 | hdfs oev -p XML -i edits_xxxx -o ./edits_xxxx.xml |
1 | hdfs oiv -p XML -i fsimage_xxxx -o ./fsimage_xxxx.xml |
EditLog 和 FsImage 在:
- NN 的
${hadoop.tmp.dir}/dfs/name/current - 2NN 的
${hadoop.tmp.dir}/data/dfs/namesecondary/current
YARN
1 | start-yarn.sh |
配置
1 | <property> |
ZooKeeper
如果你只用一台机器,应该不用装。
ZooKeeper 特点是只要有半数以上的节点正常工作,整个集群就能正常工作,所以适合装到奇数台服务器上。
配置 zkData/myid
配置 conf/zoo.cfg
1 | dataDir=/usr/local/zookeeper-3.8.2/zkData |
HBase 2.5.8
它自带 ZooKeeper 3.8.3,StandAlone 模式下只有一个 HMaster 进程:其中包括 HMaster,单个 HRegionServer 和 ZooKeeper 守护进程。
它的数据可以存在本地或 HDFS 上,这里配置存在 HDFS 上。
https://hbase.apache.org/book.html#standalone_dist
https://hbase.apache.org/book.html#shell_exercises
命令
1 | start-dfs.sh |
1 | help |
配置
如果你没有在 hbase-env.sh 里配置
JAVA_HOME,你会看到:
1 | 127.0.0.1: +======================================================================+ |
hbase-site.xml:
1 | <property> |
如果不设置 zkData 目录,它会在 /tmp/hbase-yourname
下。
第三个配置项是为了解决:参见 https://hbase.apache.org/book.html#wal.providers
1 | ERROR [RS-EventLoopGroup-3-2] util.NettyFutureUtils (NettyFutureUtils.java:lambda$addListener$0(58)) - Unexpected error caught when processing netty |
Spark 3.5.1
命令
1 | start-master.sh |
1 | spark-submit --class org.apache.spark.examples.SparkPi --master yarn $SPARK_HOME/examples/jars/spark-examples_2.12-3.5.1.jar |
1 | spark-shell --master yarn |
配置
spark-env.sh:
1 | export SPARK_DIST_CLASSPATH=$(/opt/hadoop-3.3.6/bin/hadoop classpath) |
workers:
1 | localhost |
Hive 4.0.0
https://developer.aliyun.com/article/632261
Hive 的数据默认存在 HDFS 里,元数据可以存在 MySQL 上。
分外部表和内部表。内部表默认存在 HDFS,外部表可以存在 HBase 里。
配置元数据存在 MySQL 上
https://www.mysqltutorial.org/getting-started-with-mysql/install-mysql-ubuntu/
1 | sudo systemctl start mysql.service |
把 MySQL 驱动程序 https://dev.mysql.com/downloads/connector/j/ JAR
包复制到 $HIVE_HOME/lib
hive-site.xml:
1 | <property> |
1 | schematool -dbType mysql -initSchema |
1 | mysql -u root -p |
启动 MySQL、DFS、YARN 和 HiveServer2,再用 beeline 连接 HS2
它的日志默认在 ${java.io.tmpdir}/yourname/hive.log
1 | java -XshowSettings:properties -version |
运行建表脚本:
1 | 0: jdbc:hive2://localhost:10000/> !run /path/to/create_table1.hql |
执行 HQL:
1 | 0: jdbc:hive2://localhost:10000/> show tables; |
创建内部分区表
它的 LOAD DATA INTO TABLE 操作会调用 MapReduce
加 LOCAL 是本地的,不加是 HDFS 的(?)
HQL 示例:
1 | CREATE TABLE table1 ( |
文本文件示例:
1 | 1 Alice 25 HR nanjing |
创建有结构列的内部分区表
1 | CREATE TABLE table2 ( |
1 | 1,Lilei,book;tv;code,beijing:chaoyang;shanghai:pudong |
创建外部分桶表到 HBase,用临时表数据覆写
1 | CREATE EXTERNAL TABLE table3 ( |
1 | CREATE TEMPORARY TABLE table4 ( |
重启 Hive 客户端后,临时表 table4 会消失
1 | 1:John:Male:25 |
配置
1 | java.lang.RuntimeException: Error applying authorization policy on hive configuration: java.net.URISyntaxException: Relative path in absolute URI: ${system:java.io.tmpdir%7D/$%7Bsystem:user.name%7D |
在 hive-site.xml 里把报错信息里报的开头的
system 去了
1 | java.lang.RuntimeException: java.lang.RuntimeException: org.apache.hadoop.ipc.RemoteException(org.apache.hadoop.security.authorize.AuthorizationException): User: xxx is not allowed to impersonate anonymous |
core-site.xml:
1 | <property> |
Flume 1.11.0
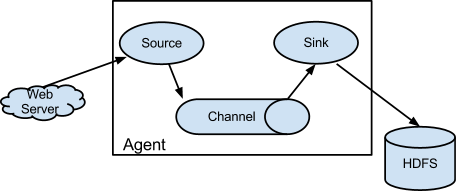
Flume 是一个水槽,用于采集、聚合和传输流数据(事件)。对于每一个代理 agent,有源 source、汇 sink、渠道 channel。
https://flume.apache.org/documentation.html
启动参数
1 | flume-ng agent --conf conf -f <配置文件路径> -n <代理名> |
注意:下面的配置不一定对。笔者不小心把配置文件夹删了,但是保留的还有配置内容截图。所以下面的实际是 OCR 过来后再修改的。之前是实验成功了的,而之后没有做过实验。
Hello(netcat 源与 logger 接收器)
1 | # 代理名为 a1 |
实时监控单个追加文件(exec 源与 hdfs 接收器)
Exec Source 在启动时运行给定的 Unix
命令,并期望该进程在标准输出时连续生成数据。使用
tail –F <filename>
命令可以看到文件末尾的实时追加。
这里监控本机的 datanode 日志,并上传到 HDFS。
1 | # 代理 |
实时监控多个新文件(spooldir 源与 hdfs 接收器)
Spooling Directory Source 监视指定目录中的新文件,并在新文件出现时解析事件。
这里监控 /opt/flume-1.11.0/upload
目录。向目录里添加文件后,上传到 HDFS。
1 | # 代理 |
实时监控多个追加文件(TAILDIR 源与 hdfs 接收器)
Taildir Source:监视指定的文件,并在检测到附加到每个文件的新行后几乎实时地跟踪它们。如果正在写入新行,则此源将重试读取它们,等待写入完成。
监控 flume 目录里的 upload 目录和 upload1 目录。
1 | # 代理 |
查看 taildir_position.json:其中 inode
号码是操作系统里文件的唯一 id,pos 是 flume
的读取到的最新的文件位置(偏移量)
Taildir source 是存在问题的:如果文件名变了,会重新上传。如果日志的文件名在一天过后变了,它会被重新上传一份。解决方案有修改 flume 的源码,或者修改生成日志文件名部分的源码。
监控 MapReduce 结果,上传到 HDFS
(1)使用 Flume 的 spooldir 源递归监控 /opt/result/
目录下的文件,汇总到 hdfs 接收器
hdfs://mycluster/flume/mrresult。
(2)将文献上传到 HDFS 的 /wcinput 目录,执行 MR
输出到本地路径 file:///opt/result/mrresult
注意:如果提前建好 MR 的输出目录,MR 会报错。而如果不提前建好 flume 的监控目录,flume 会报错。
所以只提前建好外层目录,用 flume 递归监控外层目录,MR 输出到内层目录。
1 | # 代理 |
执行 MR:
1 | hadoop jar $HADOOP_HOME/share/hadoop/mapreduce/hadoop-mapreduce-examples-3.3.6.jar wordcount /wcinput file:///opt/result/mrresult |
YARN-HA
配置
三台机器上分别都配一个 ResourceManager、NodeManager、ZooKeeper
yarn-site.xml:
| name | value |
|---|---|
| yarn.nodemanager.aux-services | mapreduce_shuffle |
| yarn.resourcemanager.ha.enabled | true |
| yarn.resourcemanager.recovery.enabled | true |
| yarn.resourcemanager.store.class | org.apache.hadoop.yarn.server.resourcemanager.recovery.ZKRMStateStore |
| yarn.resourcemanager.zk-address | ubuntu101:2181,ubuntu102:2181,ubuntu103:2181 |
| yarn.resourcemanager.cluster-id | cluster-yarn1 |
| yarn.resourcemanager.ha.rm-ids | rm1,rm2,rm3 |
| yarn.resourcemanager.hostname.rm1 | ubuntu101 |
| yarn.resourcemanager.hostname.rm2 | ubuntu102 |
| yarn.resourcemanager.hostname.rm3 | ubuntu103 |
| yarn.resourcemanager.webapp.address.rm1 | ubuntu101:8088 |
| yarn.resourcemanager.webapp.address.rm2 | ubuntu102:8088 |
| yarn.resourcemanager.webapp.address.rm3 | ubuntu103:8088 |
| yarn.resourcemanager.address.rm1 | ubuntu101:8032 |
| yarn.resourcemanager.address.rm2 | ubuntu102:8032 |
| yarn.resourcemanager.address.rm3 | ubuntu103:8032 |
| yarn.resourcemanager.scheduler.address.rm1 | ubuntu101:8030 |
| yarn.resourcemanager.scheduler.address.rm2 | ubuntu102:8030 |
| yarn.resourcemanager.scheduler.address.rm3 | ubuntu103:8030 |
| yarn.resourcemanager.resource-tracker.address.rm1 | ubuntu101:8031 |
| yarn.resourcemanager.resource-tracker.address.rm2 | ubuntu102:8031 |
| yarn.resourcemanager.resource-tracker.address.rm3 | ubuntu103:8031 |
| yarn.nodemanager.env-whitelist | JAVA_HOME,HADOOP_COMMON_HOME,HADOOP_HDFS_HOME,HADOOP_CONF_DIR,CLASSPATH_PREPEND_DISTCACHE,HADOOP_YARN_HOME,HADOOP_MAPRED_HOME |
实验
查看当前活跃节点:
1 | yarn rmadmin -getAllServiceState |
如果浏览器访问 Standby 节点的 8088 端口(RM),会自动跳转到 Active 节点。
解决 JSch 认证失败
问题出现在配置 HDFS HA 自动故障转移时。杀掉活跃的 NN 之后,它没有被隔离成功。
JSch 是一个库,它在 Java 程序里建立 SSH 连接。
在杀掉 Acitive 的 NN 过程中
被杀的 Acitive 的 NN 上的 ZKFC 日志:
- [08:38:38,534] hadoop 高可用健康监测者抛出 EOF 异常,进入 SERVICE_NOT_RESPONDING 状态
- [08:38:38,615]
- org.apache.hadoop.hdfs.tools.DFSZKFailoverController: 获取不到本地 NN 的线程转储,由于连接被拒绝
- org.apache.hadoop.ha.ZKFailoverController: 退出 NN 的主选举,并标记需要隔离
- hadoop 高可用激活 / 备用选举者开始重新选举
- [08:38:38,636] ZK 客户端不能从服务端读取会话的附加信息,说服务端好像把套接字关闭了
- [08:38:38,739] 会话被关闭,ZK 客户端上对应的事件线程被终止
- 之后 hadoop 高可用健康监测者一直尝试重新连接 NN,连不上
原来 Standby 的 NN 上的 ZKFC 日志:
- [08:38:38,719] 选举者检查到了需要被隔离的原活跃节点,ZKFC 找到了隔离目标
- [08:38:39,738] org.apache.hadoop.ha.FailoverController 联系不上被杀的 NN
- [08:38:39,748] 高可用节点隔离者开始隔离,用 org.apache.hadoop.ha.SshFenceByTcpPort,里面用了 JSch 库建立客户端(本机)与服务端(被杀的)之间的 SSH 连接
- [08:38:40,113] SSH 认证失败,隔离方法没有成功,选举失败
- 之后选举者一直在重建 ZK 连接,重新连 NN 连不上,重新隔离失败
软件版本
客户端(Standby 上的 org.apache.hadoop.ha.SshFenceByTcpPort.jsch):
- Hadoop 3.3.6 SshFenceByTcpPort 源码
- JSch 0.1.55
服务端(被杀的):
- OpenSSH_8.9p1 Ubuntu-3ubuntu0.6, OpenSSL 3.0.2 15 Mar 2022 里的 sshd
生成密钥时用的命令:
1 | ssh-keygen -t rsa -m PEM |
关键日志
原来为 Standby 的 NN 上的 ZKFC 日志:
1 | INFO org.apache.hadoop.ha.SshFenceByTcpPort.jsch: |
解决思路
看 sshd 的日志:
1 | userauth_pubkey: key type ssh-rsa not in PubkeyAcceptedAlgorithms |
1 | sudo vi /etc/ssh/sshd_config |
1 | PubkeyAuthentication yes |
1 | sudo systemctl restart sshd |
不是问题的问题
用
1 | hdfs haadmin -getAllServiceState |
查看 Active 转移成功了,但是联系不上被杀的那一方。
具体地说,转移成功之后,三个方的 DN 都一直在尝试连被杀那一方的 NN,一直在写日志。除此之外上传下载都没问题。
这应该是集群自带的心跳机制,不是问题。