数学碎片
大部分可以再认,少部分可以再现,更少部分可以迁移。
推断的有效性和可靠性
推断是前提的集合加上结论。前提最少有一句,结论只有一句。
一个推断是有效的:
- <=> 不存在当所有前提为真时,结论为假的情况
- <=> 对所有前提且的结果 => 结论
- <=> (对所有前提且的结果 -> 结论)为重言式
- 小明是人(P)
- 小明不是人(非 P)
- 因此,张三会飞(Q)
评估有效性需要把所有真值指派的情况列出来:
| P | 非 P | Q |
|---|---|---|
| 0 | 1 | 未知 |
| 1 | 0 | 未知 |
列出来后发现:不存在当所有前提为真时,结论为假的情况。所以这个推断是有效的。从矛盾的前提可以推出任何结论。
一个推断是可靠的 <=> 论证是有效的 且 它的所有前提实际为真
假言三段论是类似于这样的推断:
- A -> B
- B -> C
- 因此,A -> C
| A | B | C | A→B(前提 1) | B→C(前提 2) | A→C(结论) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
把真值表画出来之后,可以看到:当前提均为真时,结论一定为真。说明这个推断是有效的
可靠性是针对一个具体论证实例的。当 ABC 取具体的值的时候(一次真值指派),如果还能保证两个前提都是为真的,那么推断是可靠的
对于这个推断来说:
- A -> B(如果小明是湖北省出生的人,那么小明会飞)
- B -> C(如果小明会飞,那么小明的身份证以 42 开头)
- 因此,A -> C(因此,如果小明是湖北省出生的人,那么小明的身份证以 42 开头)
现在我们知道的信息是:小明确实是湖北省出生的人,身份证以 42 开头,也不会飞。那么 A=1,B=0,C=1,对应真值表的倒数第三行
首先它是有效的。其次它是不可靠的(即使它的结论为真),因为第一个前提是假的,它没有保证所有前提都为真
对于这个推断来说:
- A -> B(如果小明是湖南人,那么小明是网络小说里的人物)
- B -> C(如果小明是网络小说里的人物,那么小明会飞)
- 因此,A -> C(因此,如果小明是湖南人,那么小明会飞)
现在我们知道的信息是:小明确实是网络小说里的湖南人,会飞。那么 A=1,B=1,C=1
首先它是有效的。其次它是可靠的,因为他的所有前提都是真的(即使第一个前提看起来有点问题),结论也是真的。【AI 判定】
【AI 生成】第一个前提和结论都违背了常识,但在逻辑中,这并不影响推断的有效性或可靠性。逻辑只关心真值,而这里 A→B 的真值由小明的具体属性保证(A 真且 B 真)。A→B 的 “问题” 在于它的语义内容(内容上不现实),而非逻辑真值。逻辑只处理 “如果 A 则 B” 的真假,不处理 “为什么 A 会导致 B”。
命题逻辑
在命题逻辑中,命题用大写字母表示,它的真值只能取 0 或 1,所以也叫二值逻辑。具有确定真值的命题叫命题常元,真值不确定的命题叫命题变元。
运算符(命题连接词)优先级:非、且、或、蕴含、等值
形如 A -> B 的,叫条件命题,或者假言命题,它陈述的是某一事物情况是另一件事物情况的条件。
- 充分条件:如果 A 那么 B。A -> B 为蕴含。当蕴含的前件为假时,复合命题为真;当蕴含的前件为真时,复合命题为后件的真值;
- 充要条件:A <-> B,当 A 和 B 真值一致时,复合命题为真,否则为假
命题公式的递归定义:
- 0、1 是命题公式
- 命题变元是命题公式
- 如果 A 是命题公式,那么!A 是命题公式
- 如果 A 和 B 是命题公式,那么 (A and B)、(A or B)、(A -> B)、(A <-> B) 是命题公式
- 只有有限次利用上述四点所产生的符号串才是命题公式
真值表是对于一个命题公式,把它的命题变元的真值指派的所有情况列出来,再计算结果。
- 重言式 <=> 1(对它的所有真值指派都为 1)如 A or 1
- 矛盾式 <=> 0(对它的所有真值指派都为 0)如 A and !A
如果对命题公式 F 的真值指派中,存在一个是取值为真的,那么 F 称为可满足的公式。重言式 => 可满足的公式
命题公式的代换实例是指,对一个命题公式,把它的一个命题变元 A 用另一个公式 B 代换,且它里面的所有 A 都被 B 代换了。
代入规则:重言式的代换实例仍然是重言式。因为重言式 <=> 1,不受被代换的命题变元取值影响。
子公式是指一个命题公式的一部分(连续的几个符号),且它仍然是公式。
置换规则:对一个命题公式里 A 的子公式 B,如果用与该子公式等值的公式 C 去替代子公式 B,那么替换后得到的 D 与 A 等值。
对偶:对一个命题公式,把它的所有且或变号,01 互变,得到的新公式是原公式的对偶。
命题公式的等值关系和蕴含关系
等值关系可以双向推,蕴含关系只能从左向右推。
- 等值演算 (<=>) 像是告诉你两个数学表达式(如 (a+b)² 和 a² + 2ab + b²)在数值上总是相等的,你可以互相替换。
- 蕴含关系 (=>) 像是告诉你一条推理规则(如 “如果 a > b 且 b > c,那么 a > c”)。它定义了从已知事实推导出新事实的合法途径。反过来不一定成立
<-> 是命题连接词,经 <-> 连接后的是命题公式。而 <=> 是命题公式之间的关系符号,表示两个命题公式之间的等值关系。
A <=> B 充要条件:
- A <-> B 是永真式(<=> 的定义)
- 在任一组真值指派后,这两个公式的值一致(<-> 的定义)
=> 表示命题公式间的蕴含关系。
A => B 充要条件:
- A -> B 是永真式(=> 的定义)
- 在对他们进行的所有真值指派里,当 A 为真时,B 一定为真
- 必要性:如果 A -> B 是重言式,意味 A 和 B 的取值只可能在第 1、2、4 行里。所以说,在对他们进行的所有真值指派里,当 A 为真时,B 一定为真
- 充分性:如果对 AB 进行的所有真值指派里,当 A 为真时,B 一定为真,意味 A 和 B 的取值只可能在第 4 行里。所以 A -> B 是永真式
| A | B | A->B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
前件也可以是一个集合。若 {A,B} => C,说明:在对他们进行的所有真值指派里,当 {A,B} 中公式同时为真时,C 一定为真。对于一个推断,前提为 A 和 B,结论为 C。如果这个推断是有效的,那么 {A,B} => C,或者说(A 且 B)=> C,或者说 (A 且 B)-> C <=> 1
如何推证 A => B:有两种方法:
- 先假定 A 为真,再检查 B 的真值。如果 B 一定为真,蕴含关系成立;否则不成立。
- 先假定 B 为假,再检查 A 的真值。如果 A 不可能为真,蕴含关系成立;否则不成立。
对 P and Q => P 来说:
- 假定前件 P and Q 为真,那么 P 一定为真。所以蕴含关系成立
- 假定后件 P 为假,那么前件为假(不可能为真),所以蕴含关系成立
对 P or Q => P 来说:
- 假定前件 P or Q 为真,那么后件的真值是不确定的。所以蕴含关系不成立
- 假定后件 P 为假,那么前件的真值是不确定的(可能为真),所以蕴含关系不成立
命题公式的等值演算
- 对于两个命题,单独的或和且间有交换律,三个命题间有结合律。和乘法和加法类似
- 分配律:(A 且 B)或(A 且 C)<=> A 且(B 或 C)
- 两命题且或的运算
- 且 1 或 0 不变:同一律
- 且 0 或 1 短路:零一律
- 且自身或自身不变:等幂律
- 矛且 0,矛或 1:互否律
- 吸收律:三个命题以一且一或连接,后两个有括号,且前两个命题相同,那么它的值为第一个命题的值
- P 蕴含 Q <=> 非 P 或 Q <=> (P 蕴含 Q) 且 (Q 蕴含 P)
- P 等值 Q:析取范式,非号聚集;合取范式,非号分散

- 对命题公式 A 最外面加非 <=> 把 A
的对偶公式里的所有命题变元加非
- 德摩根律:多个命题以且 / 或连接,括号外有一个非,那么可以把非分配到括号里的各个命题上,并把且或变号
通过命题公式的等值演算证明,一对矛盾的前提可以推出任何结论:

范式
当我们说 ^A 的主?[析合] 取范式是 B$ 的时候,意味着 A<=>B。
析取就是或,合取就是且。
- 质合取式:由命题变元或其否定以连且的方式连接到一起。P and Q and !R
- 质合取式是矛盾式的充要条件是,它里面同时含有一个命题变元及其否定
- 充分性:矛且为 0,0 且短路
- 必要性:假设质合取式中没有同时含有一个命题变元及其否定,那么总能指派真值使得它每个部分全 1,整体为 1 不矛盾,假设不成立
- 质析取式:由命题变元或其否定以连或的方式连接到一起。P or Q or !R
- 质析取式是重言式的充要条件是,它里面同时含有一个命题变元及其否定
- 充分性:矛或为 1,1 或短路
- 必要性:假设质合取式中没有同时含有一个命题变元及其否定,那么总能指派真值使得它每个部分全 0,整体为 0 不重言,假设不成立
- 析取范式:外层是析取,内层是质合取式。(且且)或(且且)或(且且)
- 合取范式:外层是合取,内层是质析取式
任一公式都可变换成与它等值的析取范式或者合取范式,可能不止一种。变换的过程:
- 把蕴含改写成:非 P 或 Q,等值改写成:析取范式非号聚集;合取范式非号分散
- 用德摩根律把括号外的否定号向内深入到命题变元身上
- 用双重否定律消去非非
- 用分配律把:
- P 且(Q 或 R)变成(P 且 Q)或(P 且 R)的析取范式
- P 或(Q 且 R)变成(P 或 Q)且(P 或 R)的合取范式
- 由一些命题变元产生的最小项,是类似于连且的质合取式,但是没有重复的变元。如对于命题变元
A 和 B, A 且 非 A 且 B 是一个质和取式,但不是最小项。最小项类似 A 且 非
B
- 对所有最小项进行真值指派,在每次真值指派里,有且只有一个最小项取值为 1
- 对某一个最小项进行真值指派,在所有真值指派里,有且只有一次取值为 1
- 由一些命题变元产生的最大项,是类似于连或的质析取式,但是没有重复的变元。
- 主析取范式:由不同最小项为质合取式形成的析取范式。如变元 A、B 的其中一个主析取范式是:(A 且 B)或(非 A 且 B)
- 主合取范式:由不同最大项为质析取式形成的合取范式。如变元 A、B 的其中一个主合取范式是:(A 或 B)且(A 或 非 B)
A 是重言式:
- <=> A
的合取范式中(外层连且)每一质析取式(内层连或)都至少有一对矛盾的命题变元
- 充分性:矛或为 1,内层短路,全且 1 为 1
- 必要性:假设 A 的某一质析取式 Ai 不包括互矛的,那么 Ai 不是重言式,进而存在一组真值指派使 Ai 为假,外层连且短路为假,与 A 是永真式矛盾,假设不成立
- <=> A 的主析取范式中出现了所有最小项
- 充分性:对它的所有最小项进行一次真值指派后,必定是一个真而其他全假,因为最小项是连且的,只有一种情况取 1。1 在连或中短路,所以主析取范式为重言式
- 必要性:假设 A 的主析取范式中没有出现所有最小项,至少漏了一个,那么对于某次真值指派,可能恰好为漏的那一项为 1,其他项都为 0 的情况,造成析取的结果是 0,与 A 是重言式矛盾,假设不成立
A 是矛盾式:
- <=> A
的析取范式中(外层连或)每一质合取式(内层连且)都至少有一对矛盾的命题变元
- 充分性:矛且为 0,内层短路,全或 0 为 0
- <=> A 的主析取范式是空公式 0

直言三段论
直言三段论由三个直言命题组成,AAA-1 的直言三段论是这样的:
- 所有 M 是 P
- 所有 S 是 M
- 因此,所有 S 是 P
在结论中的主词记为 S 是小项,谓词记为 P 是大项。包括 P 的前提是大前提,包括 S 的前提是小前提。没有出现在结论里,而在两个前提里重复出现的是中项 M。
| 肯定:谓项都不周延 | 否定:谓项都周延 | |
|---|---|---|
| 全称:主项都周延 | A:所有主 + 是谓 -,主包含在谓里 | E:没有主 + 是谓 +,主谓互斥 |
| 特称:主项都不周延 | I:有些主 - 是谓 -,主谓有交 | O:有些主 - 不是谓 +,主不包含在谓里 |
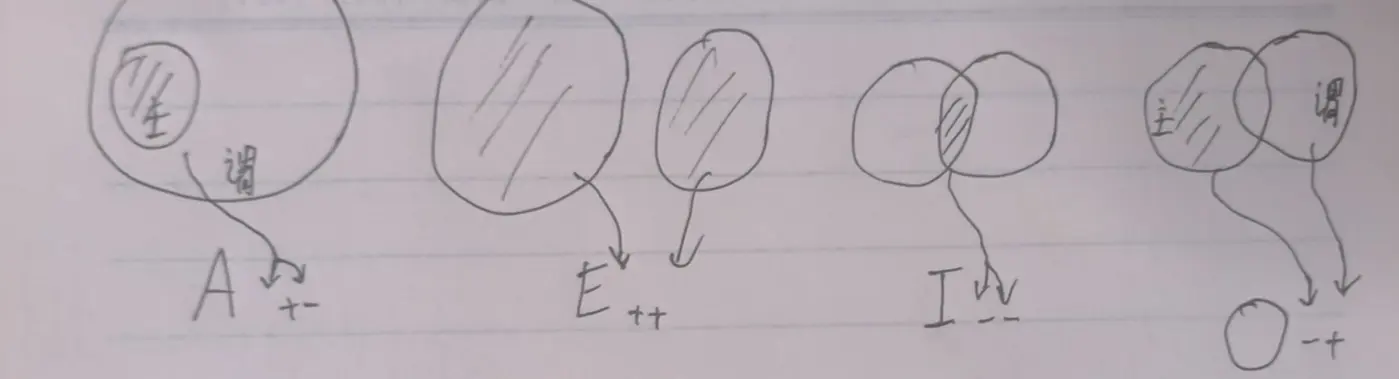
周延指的是,一个词项涵盖了他的所有外延。+ 记为周延,- 记为不周延。
小明是只有一只脚的;小明是人;因此,人是只有一只脚的
在它的结论中人是周延的,指的是所有人。而在小前提中的人是没有周延的,只包括小明一个人。
当我们说 “A 是 B” 的时候,往往意味着 A 在 B 的范围内,A 是 B 的一部分;说 “A 不是 B” 的时候,往往意味着 A 一点都不在 B 里面。
所以说肯定判断的谓项都不周延,否定判断的谓项都周延。
- 肯定判断的谓项都不周延:所有武汉人 + 都是科学家 -(全肯 A),或有些武汉人 - 是科学家 -(特肯 I),这里的科学家没有周延到所有科学家
- 否定判断的谓项都周延:所有武汉人 + 都不是科学家 +(全否 E),或有些武汉人 - 不是科学家 +(特否 O),这里的科学家周延到了所有科学家
- 特称判断的主项都不周延:因为是以有些…… 开头的
- 全称判断的主项都周延:因为是以所有 / 没有…… 开头的。单称命题主词包括的对象只有一个,所以也周延
格指的是,在大前提和小前提中,大项、小项和中项的排列顺序。结论的顺序一定是 S-P,小项 - 大项
- 第 1 格:中项一左一右,是分开的。大前提 M-P,小前提 S-M
- 第 2 格:中项都在右边。大前提 P-M,小前提 S-M
- 第 3 格:中项都在左边。大前提 M-P,小前提 M-S
- 第 4 格:中项一右一左,是聚集的。大前提 P-M,小前提 M-S
小明只有一只脚;小明是人;因此,人只有一只脚
它的中项都在左边,所以是第三格。全肯 A,AAA-3 属于无效推理
一个 EIO-2 的有效的(但不可靠的)三段论是这样的:
- 没有安徽人是科学家(全否 E)
- 有些中国人是科学家(特肯 I)
- 因此,有些中国人不是安徽人(特否 O)
如果把科学家替换成湖北人,就是有效且可靠的。
如何判断三段论有效性:需要满足下列的所有规则。或者画韦恩图,或者查表
- 结论中否定命题的数目必须和前提中否定命题的数目相等
- 结论中特称命题的数目必须和前提中特称命题的数目相等
- 结论中周延的词必须在前提中周延
- 中项必须周延至少一次
如果语境上不能假设所有提及的集合非空,部分推论将会无效。
形式谬误
形式谬误的推理过程是无效的。
有效的选言三段论是这样的:也叫析取三段论,或拒取式。
- P 或 Q
- 非 P
- 所以 Q
它对应肯定选言的谬误:
- P 或 Q
- P
- 所以 Q 为假
命题逻辑谬误
手电筒发光有两个条件:电池有电,且开关打开了。
- 肯定后件:如果手电筒发光了,那么它是有电的;手电筒是有电的;因此手电筒正在发光
- 否定前件:如果手电筒发光了,那么它是有电的;手电筒没有发光;因此手电筒是没电的
发现肯定后件、否定前件、肯定选言、否定联言的方式都是:通过真值表的复合命题列,加上简单命题其中的一列,找另一个简单命题列在真值表里有两种的情况,强制把它推向其中一种。如:
| P:手电筒正在发光 | Q:它的电池有电 | 蕴含:若手电筒正在发光,则它的电池有电 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- “若 P 则 Q” 为真时
- P 为假时,Q 有两种情况(否定前件谬误:若 P 则 Q 为真,P 为假,推出 Q 为假)
- P 为真时,Q 只有一种情况(这是有效的,肯定前件的推理。手电筒正在发光,说明它的电池一定有电)
- Q 为假时,P 只有一种情况(这是有效的,否定后件的推理。手电筒的电池没电,说明它一定不会发光)
- Q 为真时,P 有两种情况(肯定后件谬误:若 P 则 Q,Q,因此 P)
过去的碎片
我们用 \(m\) 表示样本数量,与维度 \(n\) 区分开。用 \(d\) 表示属性的个数。
粗斜体小写字母为列向量,如 \(\boldsymbol{x}=(1;2;3)\),使用分号分隔。其转置为行向量,使用逗号分隔。
粗斜体大写字母为矩阵。在上下文明确的情况下可不用粗体。
在上下文明确的情况下可省略求和符号的起止。
概率论与数理统计知识
\(\sum x_i = m\bar{x}\)
离散型随机变量函数的期望 \(E(f(X))\):参考。\(f\) 是连续函数且级数绝对收敛,\(E(f(X)) = \sum P(x_i)f(x_i)\)
离散型随机变量的信息熵 \(H(X)\):
信息量 \(I(x_i) = - \log_2{P(x_i)}\):投一次正八面体骰子(0-7 点),有概率均等的八种结果。把每种结果都用 3 bit 的二进制数表示,熵为 3 bit。
- 信息 “结果是 1 点” 的信息量是 3 bit,得到这个信息之后,熵剩余 0 bit
- 信息 “结果是 1 点或 2 点的其中之一” 的信息量是 2 bit,得到这个信息之后,熵剩余 1 bit
- 信息 “结果是 1、2、3、4 点的其中之一” 的信息量是 1 bit,得到这个信息之后,熵剩余 2 bit
信息熵 \(H(X) = E(I(X)) = - \sum p_i \log_2 p_i\)。
- 投一次正八面体骰子,点数结果的信息熵是 3 bit
- 投一次 1% 概率为正面,99% 概率为反面的不均匀硬币,面结果的信息熵约 0.08 bit
- 投一次 25% 概率为正面,75% 概率为反面的不均匀硬币,面结果的信息熵约 0.811 bit
多重集合的信息熵:可能的最小值(全同)为 0,最大值(全异)为 log2 唯一值数量。
\(A = \{ 1,2,2,2 \}\)
\(H(A) \approx 0.811\)
多重集合划分后的信息熵:如把多重集合 \(\{ 1,2,2,2 \}\) 划分成两个子集 \(\{1\}\) 和 \(\{2,2,2\}\) 后,信息熵变为 \(0\)。其划分后的信息熵定义为各个子集熵的加权和,权为子集容量占原集合的比例。划分后减少的信息熵称为划分后的信息增益。
基尼指数:可能的最小值(全同)为 0,最大值(全异)为 1 - 唯一值数量的倒数。
\(A = \{ 1,2,2,2 \}\)
\(G(A) = 1- \sum p_i^2 = \frac{3}{8}\)
类似地,划分后的基尼指数定义为各个子集基尼指数的加权和,权为子集容量占原集合的比例。
线性代数知识
- \(\boldsymbol{a}^T \boldsymbol{b} = \boldsymbol{b}^T \boldsymbol{a}\)
- \((\boldsymbol{A} + \boldsymbol{B})^T = \boldsymbol{A}^T + \boldsymbol{B}^T\)
- \((\boldsymbol{AB})^T = \boldsymbol{B}^T\boldsymbol{A}^T\)
- 矩阵和向量乘法分配律注意保证顺序不变,因为没有乘法交换律
- 积的求和可以改写成两向量相乘 \(\sum_{i=1}^m x_iy_i = \boldsymbol{x}^T\boldsymbol{y}\)
- 遇到 “行向量乘列向量加标量” 的形式,可以把标量拆分成 1 和它本身,再分别补到前面那两个向量的尾巴上
- \(\boldsymbol{A}\boldsymbol{b} = \boldsymbol{c}\)
- \(\boldsymbol{a}^T \boldsymbol{B} = \boldsymbol{c}^T\)
- 行列式为零、非满秩、不可逆的方阵称为奇异矩阵
- 矩阵的秩:变换为行阶梯型矩阵后的非零行数
矩阵和行列式的几何意义:
矩阵可表示多个向量:
- 二阶行列式的绝对值是矩阵的两个列向量所张成的平行四边形的面积;
- 三阶行列式的绝对值是矩阵的三个列向量所张成的平行六面体的体积;
- 矩阵的秩是各向量张成空间的维数
矩阵可表示对一个空间基(单位格子)的线性变换:
- 用变换矩阵左乘一个向量,就是把该向量所在的空间做了变换。新坐标在旧空间里的位置与旧坐标在新空间里的位置一致。变换矩阵的行列式为新空间的单位格子相对于旧空间单位格子的面积 / 体积改变的倍数。
- 行列式为零说明是降维打击,损失了信息,变换不可逆。
- 行列式为负说明空间的手性改变了
方阵的余子式 \(M_{ij}\) 和代数余子式 \(A_{ij}\):它们都是行列式,可以求值。
- 余子式为划掉原方阵第 \(i\) 行 \(j\) 列后剩余的方阵的行列式。
- 代数余子式为余子式加一个正 / 负号,看 \(i+j\) 是偶数还是奇数。
方阵的顺序主子式:一个正方形框从左上角开始拉。它们都是行列式,可以求值。
方阵的伴随矩阵 \(A^*\):它是这样一个矩阵:新矩阵上每个位置的元素是原矩阵的一个代数余子式,代数余子式的下标和新矩阵位置的下标行列互换。对于二阶矩阵,它的伴随矩阵是主交换、副取反。
方阵的逆矩阵 \(A^{-1}\):等于伴随矩阵乘上行列式的倒数。
高斯 - 若尔当方法:把增广矩阵 \(A|I\) 初等行变换为 \(I|A^{-1}\)
方阵的特征值 \(\lambda\) 和特征向量:
- 方阵左乘它的特征向量,等于把这个特征向量在它的方向上伸缩 / 反转 \(\lambda\) 倍。
- 如何求特征值:令特征多项式 \(|\lambda \boldsymbol{E} - \boldsymbol{A}| = 0\)
- 如何求特征向量:求 \((\lambda \boldsymbol{E} - \boldsymbol{A})\boldsymbol{x} = \boldsymbol{0}\) 的基础解系
- 如何求基础解系:初等行变换成行最简型
\[ \begin{pmatrix} \boldsymbol{E}_r & \boldsymbol{F} \\ 0 & 0 \end{pmatrix} \]
解矩阵为
\[ \begin{pmatrix} - \boldsymbol{F} \\ \boldsymbol{E}_{n-r} \end{pmatrix} \]
正定矩阵充要条件:其所有特征值都为正。或者所有顺序主子式为正。
正交矩阵:\(AA^T = E\)。正交矩阵的各行是单位向量且两两正交,各列是单位向量且两两正交。
矩阵的奇异值分解是把一个矩阵分解成三个矩阵相乘:
\[ A = U \Sigma V^T \]
\(A\) 是实矩阵的情况下,\(U\) 和 \(V^T\) 都是正交矩阵,\(\Sigma\) 是与 \(A\) 形状相同的对角矩阵,其对角线上的元素叫奇异值,呈非负且按降序排列。
如何分解:\(U\) 的每一列是 \(AA^T\) 的特征向量,\(V\) 的每一列是 \(A^TA\) 的特征向量,\(\Sigma\) 对角线上每一个元素是 \(A^TA\) 或 \(AA^T\) 的特征值开根号,注意保证各奇异值和特征向量对应。
高数知识
复合函数求导法则:把内层的中介写一遍,连乘
Sigmoid 函数(对数几率函数):\(S(x) = \dfrac{1}{1+e^{-x}}\),该函数图像长得和 \(\dfrac{1}{\pi} \arctan x + \dfrac{1}{2}\) 差不多
\[ \dfrac{1}{1+a^{-x}} + \dfrac{1}{1+a^{x}} = 1 \]
\(n\) 元函数 \(f(\boldsymbol{x})\):自变量有 \(n\) 个,记作一个 \(n\) 维列向量 \(\boldsymbol{x}\)。
梯度(一阶导数) \(\nabla f(\boldsymbol{x}) = \dfrac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}\)
梯度是一个 \(n\) 维向量,各个分量是原函数在其各个自变量分量上的偏导函数 \(\dfrac{\partial f(\boldsymbol{x})}{\partial {x_i}}\),前提是各个偏导数都存在。如:
\[ \nabla (5x_1+4x_1x_2+x_3) = (5+4x_2,4x_1,1) \]
海森矩阵(二阶导数) \(\nabla^2 f(\boldsymbol{x}) = \dfrac{\partial^2 f(\boldsymbol{x})}{\partial \boldsymbol{x}{\partial \boldsymbol{x}}^T}\):海森方阵的每一个元素是原函数的二阶偏导数,前提是各个二阶偏导数都存在。如:
\[ \nabla^2(2x_1 + x_1x_2) = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \]
凸函数:这里的凸函数指下凸函数。
凸函数任意两点的连线一定在函数图像上面,或与函数图像重合。如果一定在上面,我们称它为严格的凸函数。
一元严格凸函数的例子:\(y = x^2\)
一元非严格凸函数的例子: \(y = x + 1\)
如何判定一元函数是凸函数 / 严格凸函数:其二阶导数在区间上恒大于等于 / 大于零
如何判定多元函数是凸函数 / 严格凸函数:其海森矩阵在区间上是半正定 / 正定的
矩阵微分公式:
\(\frac{\partial \boldsymbol{a}^T \boldsymbol{x}}{\partial \boldsymbol{x}} = \frac{\partial \boldsymbol{x}^T \boldsymbol{a}}{\partial \boldsymbol{x}} = \boldsymbol{a}\) (南瓜书)
\(\frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}^T} = \boldsymbol{A}\) (南瓜书)
\(\frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}} = \boldsymbol{A}^T\) (https://en.wikipedia.org/wiki/Matrix_calculus 的分母布局)
\(\frac{\partial \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}} = (\boldsymbol{A} + \boldsymbol{A}^T) \boldsymbol{x}\)(南瓜书)
一元线性回归
目的:找出与平面直角坐标系上的 \(m\) 个散点 \((x_i,y_i)\) 最接近的直线 \(\hat{y} = wx+b\)
找出使残差平方和最小的直线的斜率、截距,即求:
\[ (w^*,b^*) = \underset{(w,b)}{\mathrm{arg\ min}} \sum_{i=1}^{m} (y_i-wx_i-b)^2 \]
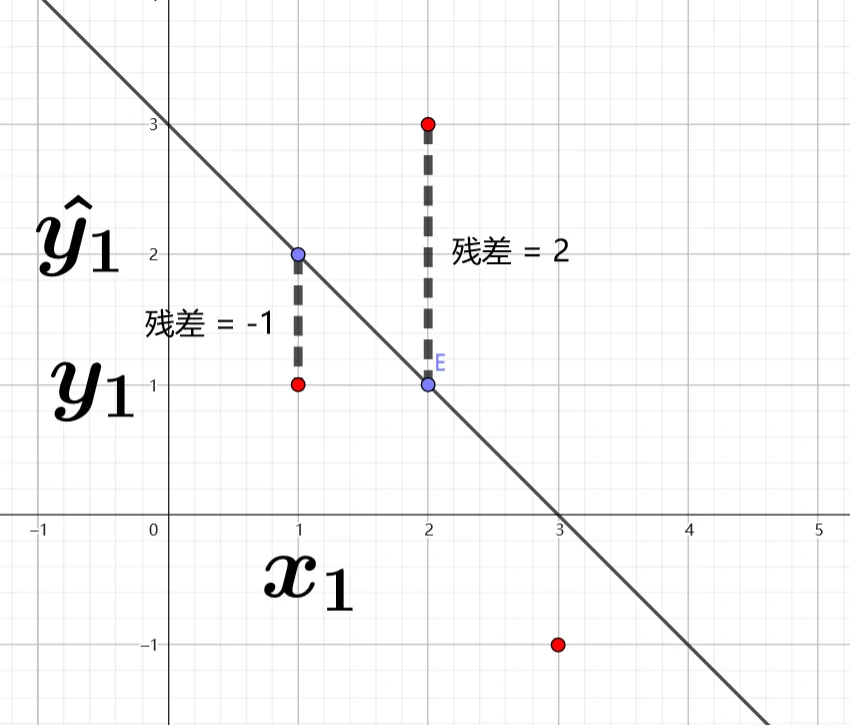
观测值(已知的,用于训练模型的样本 \(y\) 值):\(y_i\)
估计值(给定一个 \(x_i\) 用模型 \(\hat{y} = wx+b\) 算出来的值):\(\hat{y_i}\)
残差:\(y_i-\hat{y_i} = y_i-wx_i-b\)
这个公式是高中数学的内容,可以写成向量形式:
\[ \begin{aligned} w &= \frac{\boldsymbol{x}^T\boldsymbol{y} - m\bar{x}\bar{y}} {\boldsymbol{x}^T\boldsymbol{x}-m\bar{x}^2} = \frac{\boldsymbol{x}_d^T \boldsymbol{y}_d}{\boldsymbol{x}_d^T \boldsymbol{x}_d} \\ b &= \bar{y} - w\bar{x} \end{aligned} \]
\(\boldsymbol{x}_d\) 的各个分量是 \(x_i - \bar{x}\)
公式是怎么来的:
- 残差平方和是关于 \(w\) 和 \(b\) 的二元函数,其海森矩阵为:
\[ \begin{pmatrix} 2 \sum_{i=1}^m x_i^2 & 2 \sum_{i=1}^m x_i \\ 2 \sum_{i=1}^m x_i & 2m \end{pmatrix} \]
只要有一个非零的 \(x\) 值,它的一阶主子式就为正;由柯西不等式的一般形式,只要有不相等的 \(x\),它的二阶主子式就为正。做一元线性回归至少需要三个不同的点,如果所有 \(x\) 值相同,或者都为零,就不用这个公式算了。只要用这个公式算,它的海森矩阵就是正定的,它是严格凸函数。
- 令梯度等于零向量,改写成用矩阵求解线性方程组的形式
- 两边左乘系数矩阵的逆矩阵,得到 \((w;b)\)
- 把 \(w\) 的分子分母同时除以 \(m\)
- 目标直线必定过均值点
多元线性回归
目的:找出 \(n+1\) 维欧式空间里与 \(m\) 个散点最接近的超平面:
\(f(\boldsymbol{x}) = \boldsymbol{w}^T \boldsymbol{x} + b\) 的各项参数
注意:这里的所有自变量(元)是一个 \(n\) 维向量 \(\boldsymbol{x}\)。\(\boldsymbol{w}\) 是各个一次项的系数。函数的解析式是个一次多项式
“最接近” 也可表示为 \(f(\boldsymbol{x}_i) \simeq y_i\),即用模型算出来的值几乎等于观测值。
“行向量乘列向量加标量” 的形式,把标量 \(b\) 拆分成 \(b\) 和 \(1\),写到前面那两个向量的尾巴上。记 \(\hat{\boldsymbol{w}} = (\boldsymbol{w};b)\),\(\hat{\boldsymbol{x}} = (\boldsymbol{x};1)\),则:
\[ f(\boldsymbol{x}) = \hat{\boldsymbol{w}}^T \hat{\boldsymbol{x}} = \hat{\boldsymbol{x}}^T \hat{\boldsymbol{w}} \]
公式:
当 \(\boldsymbol{X}^T\boldsymbol{X}\) 为正定矩阵时,\(\hat{\boldsymbol{w}}\) 的全局最优解为:
\[ (\boldsymbol{X}^T\boldsymbol{X})^{-1} \boldsymbol{X}^T\boldsymbol{y} \]
此时的模型为:
\[ f(\hat{\boldsymbol{x_i}}) = \hat{\boldsymbol{x}}_i^T (\boldsymbol{X}^T\boldsymbol{X})^{-1} \boldsymbol{X}^T\boldsymbol{y} \]
公式是怎么来的:
找出使残差平方和 \(E_{\hat{\boldsymbol{w}}}\) 最小的各项的系数与常数项向量 \(\hat{\boldsymbol{w}}^*\),即求:
\[ \underset{\hat{\boldsymbol{w}}}{\mathrm{arg\ min}} \sum_{i=1}^{m} (y_i - \hat{\boldsymbol{x}}_i^T \hat{\boldsymbol{w}})^2 \]
平方求和可改写成向量相乘,把括号里的向下影分身:
\[ E_{\hat{\boldsymbol{w}}} = \sum_{i=1}^{m} (y_i - \hat{\boldsymbol{x}}_i^T \hat{\boldsymbol{w}})^2 = (\boldsymbol{y} - \boldsymbol{X} \hat{\boldsymbol{w}})^T (\boldsymbol{y} - \boldsymbol{X} \hat{\boldsymbol{w}}) \]
这里影分身后的 \(\boldsymbol{y}\) 和 \(\boldsymbol{X}\) 都有 \(m\) 行,\(\boldsymbol{X}\) 的每一行为 \(\hat{\boldsymbol{x}}_i^T\)
把 \(E_{\hat{\boldsymbol{w}}}\) 展开,再对 \(\hat{\boldsymbol{w}}\) 求导得:
\[ \nabla E_{\hat{\boldsymbol{w}}} = 2 \boldsymbol{X}^T (\boldsymbol{X} \hat{\boldsymbol{w}} - \boldsymbol{y}) \]
\(E_{\hat{\boldsymbol{w}}}\) 的海森矩阵是一阶导数再对 \(\hat{\boldsymbol{w}}^T\) 求一次导:
\[ \nabla^2 E_{\hat{\boldsymbol{w}}} = 2 \boldsymbol{X}^T \boldsymbol{X} \]
当海森矩阵为正定矩阵时,\(E_{\hat{\boldsymbol{w}}}\) 为严格凸函数。令梯度等于零向量,求得的全局最优解为当 \(E_{\hat{\boldsymbol{w}}}\) 取最小值时的 \(\hat{\boldsymbol{w}}\)
梯度下降法
梯度下降法是用来逼近函数取极小值时的点的。
以一元下凸函数 f (x) 为例,在右侧任意取一个 x 值,函数图像在该点处下降最快的方向是该点的导数方向,且导数为正,此时需要向左逼近,把 x 值变小;如果一开始在左侧取,则导数为负,需要向右逼近,把 x 值变大。
我们可以规定新取的 x 值等于上一步的 x 值减去一个与它的导数符号相同的数,这样就可以保证新的取值是一定沿着上一步相对于极小值的下降方向。
方向确定了,但是可能会移动过头。由于越平缓的地方导数绝对值是越小的,为了使移动的幅度与平缓程度相称,于是我们可以规定减去的那个数等于导数乘上另一个固定的正实数。
用梯度下降法求方程的解,即求一个 x 使得函数 f (x) = 0 。我们为了判断何时问题已经解决地足够好了,可以定义一个损失函数,它是用来量化离解决一个问题还有多长距离的量。
最终目的是让求的 x 值使得 f (x) 的值更接近 0,为了量化更接近零的程度,我们可以用原函数的平方作为损失函数。于是问题转化成了用梯度下降法求损失函数的极小值点。
在编写程序的时候,计算一个点的导数,我们可以采用计算与它相邻极近两点的割线斜率。
十进制与 K 进制小数互转
K 转 10:每一位分别乘上 K 的次方,再相加。
2 转 10
有限小数
\(11.1011\mathrm{B} = 3.6875\)
| 项 | 值 |
|---|---|
| \(1\times2^{1}\) | \(2\) |
| \(1\times2^{0}\) | \(1\) |
| \(1\times2^{-1}\) | \(0.5\) |
| \(0\times2^{-2}\) | \(0\) |
| \(1\times2^{-3}\) | \(0.125\) |
| \(1\times2^{-4}\) | \(0.0625\) |
| 总和 | \(3.6875\) |
无限循环小数
\(1.1 \dot{0} 11 \dot{0} ... \mathrm{B} = 1.7\)
可以转换成分数计算:
\[ \begin {aligned} 1.1 \dot {0} 11 \dot {0} ... \mathrm {B} & = x \\ 11.\dot {0} 11 \dot {0} ... \mathrm {B} & = 2x \\ 110110. \dot {0} 11 \dot {0} ... \mathrm {B} & = 32x \\ 两式相减,110011\mathrm {B} & = 30x \\ x & = \frac {110011\mathrm {B}}{30} = \frac {51}{30} = 1.7 \end {aligned} \]
10 转 K:
整数部分仍然除 K 取余,小数部分乘 K 取整,然后相加。
10 转 2
\(0.7 = 0.1 \dot{0} 11 \dot{0} ... \mathrm{B}\)
| 小数部分乘 2 | 取整数部分 |
|---|---|
| \(0.7 \times 2 = 1.4\) | \(1\) |
| \(0.4 \times 2 = 0.8\) | \(0\) |
| \(0.8 \times 2 = 1.6\) | \(1\) |
| \(0.6 \times 2 = 1.2\) | \(1\) |
| \(0.2 \times 2 = 0.4\) | \(0\) |
| ... | ... |
10 转 16
\(0.7 = 0.\mathrm{B} \dot{3} ... _{16}\)
| 小数部分乘 16 | 取整数部分 |
|---|---|
| \(0.7 \times 16 = 11.2\) | \(\mathrm{B}\) |
| \(0.2 \times 16 = 3.2\) | \(3\) |
| ... | ... |
离散数学
基础不牢。虽然之前及格了,但是什么都没学会。
集合 A 的所有子集组成的集合,是集合 A 的幂集。{1,2} 的幂集是
{{},{1},{2},{1,2}}。
空集的幂集是 {{}} ,基数是 1。A
的幂集的基数 > A 的基数。
元素都是集合的集合,称为集族。
关系
集合:所有 \((10,60)\) 岁的人是一个集合 \(A\),所有 \((30,80)\) 岁的人是一个集合 \(B\)。当然有人同时属于这两个群体,也有同时不属于的。
笛卡尔积:把 \(A\) 放到左边,\(B\) 放到右边。把左边的所有人和右边的所有人多对多配对,用一根根线连起来。这些所有线的集合叫笛卡尔积 \(A \times B\)。当然也有自己连自己的,以及连了两次、左右互换的。注意,这些线是有方向的,是从左往右连,即 \(A \times B \not\equiv B \times A\)
关系:从这些线里任意取几根,或者全取,或者一根都不取。取出来的这几根线叫关系,记作 \(\rho\)。即关系是笛卡尔积的子集。\(\rho \subseteq A \times B\)。\(\rho\) 是从 \(A\) 到 \(B\) 的一个关系,也是有顺序的。如果取出来的这几根线左边全是老师,线右边全是对应老师的学生,则 \(\rho\) 是从 \(A\) 到 \(B\) 的师生关系。张三在左边的 \(A\) 里面,代号是 \(a\),李四在右边的 \(B\) 里面,代号是 \(b\),连接它们的线记作 \((a,b)\)。如果这条线在 \(\rho\) 里面,则记作 \(a \rho b\)。即张三对李四有师生关系 \(\rho\),张三是李四的老师。不止他们两个人在师生关系 \(\rho\) 里面。张三对李四的这根线,在取出来的线集 \(\rho\) 里面。这些线的集合才叫关系,而 \((a,b)\) 不叫关系,再起码也得 \(\{(a,b)\}\)。即 \(a \rho b\) 的意思是 \((a,b) \in \rho\), \((a,b)\) 这根线在 \(\rho\) 这个线集里面。
定义域和值域:现在有一个从 \(A\) 到 \(B\) 的师生关系 \(\rho\),就是从 \(A\) 到 \(B\) 有一些线。被师生关系牵住的左边的所有人(老师),称为这个师生关系的定义域。右边的所有人(学生),称为这个师生关系的值域。这个师生关系是建立在 \(A\) -> \(B\) 这两个群体之上的。
逆关系:从 \(B\) 到 \(A\) 的生师关系。记作 \(\tilde{\rho}\)。是 \(A\) 的各个序偶反过来写。
集合 \(A\) 上的关系:这两边可以放同一个集合,即从 \(A\) 到 \(A\) 的关系 \(\rho\),直接叫集合 \(A\) 上的关系。即单个群体内部之间的线,包括自己连自己。
前面说了,关系 \(\subseteq\) 笛卡尔积。对于 \(A\) 和 \(A\) 的笛卡尔积,两边交换位置是相等的,可以记作 \(A^2\)。集合 \(A\) 上的关系 \(\rho \subseteq A^2\)。注意在此时,不一定有 \(\rho = \tilde{\rho}\)。如果 \((你,她)\in \rho\) 且 \(\rho\) 是暗恋 ,不能保证 \((你,她)\in \tilde {\rho}\)。你对别人有暗恋关系,不能保证你对别人有暗恋关系的逆。

普遍关系 \(U_A\):所有人都连上线了,包括和自己。即这个关系等于笛卡尔积 \(A^2\)。大家
恒等关系 \(I_A\):所有人都和自己连上线了,但是互相之间没有线。我
具有特定性质的关系:
- 自反的:对于所有 a,必须都和自己有关系。所有人都和自己连上线了,不一定和对方连不连。关系矩阵主对角线上都是 1。对于集合 A,如果它上的关系 rho 是自反的,那么 rho 里的序偶里一定有 A 的所有元素各个复读一遍
- 反自反的:对于所有 a,都不能和自己有关系。所有人都不和自己连线,不一定和对方连不连。没有复读的
- 对称的:对于所有 ab,如果 a 对 b 有关系,b 一定对 a 有关系。所有连线都是双向的,或者自环。关系矩阵关于主对角线对称。对于所有的 ab,如果有 (a,b),那么一定有 (b,a)
- 反对称的:对于所有 ab,如果 a 对 b 有关系,且 b 对 a 有关系,那么 ab 一定相等。不存在双向的连线(但可以自环)。关系矩阵关于主对角线反对称,对应对称位置的值相反。对于不等的 ab,如果有 (a,b),那么一定没有 (b,a)
- 恒等关系既是对称的,也是反对称的。因为它是集合里所有元素的自环。
- 可传递的:对于所有 abc,如果 a 对 b 有关系,b 对 c 有关系,那么 a 和 c 必须有关系。对于任意一条长度为 2 的连续(同向)路径,它的起点必须可以直接通往终点。
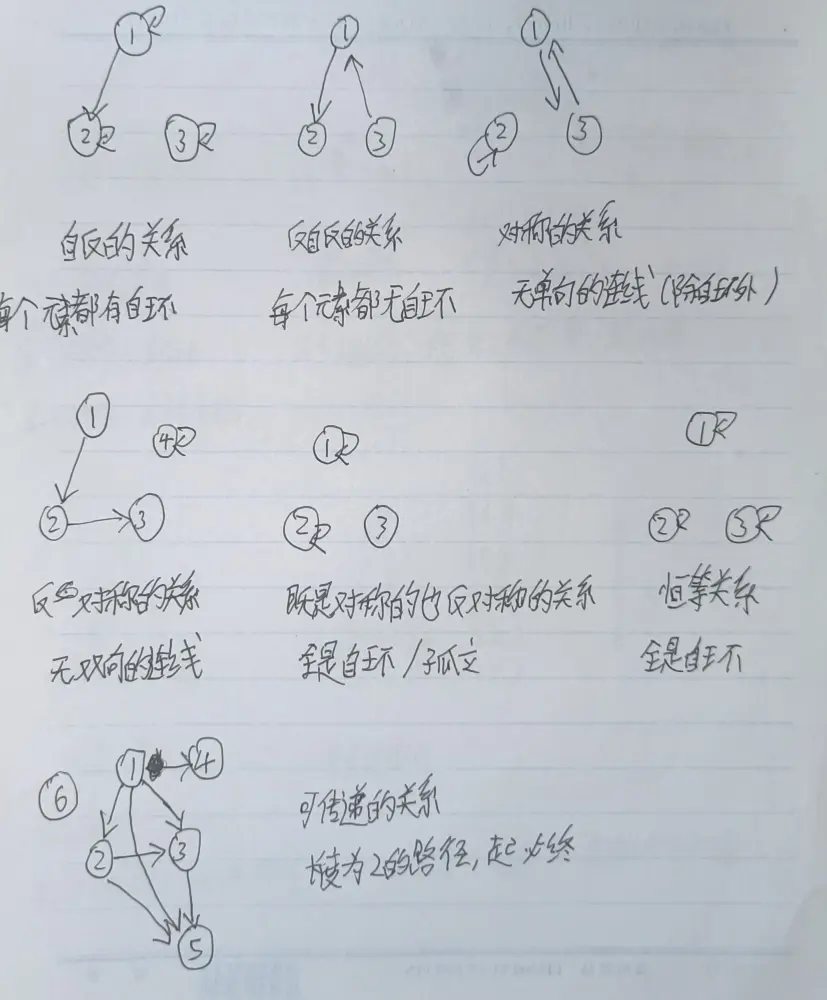
在非空集合上,一个自反关系一定不是反自反的,一个对称关系可能也是反对称的
在空集上,空关系同时是自反、反自反、对称、反对称、可传递的。由于没有元素,条件 “空真” 地成立
等价关系是自反、对称且可传递的关系。
偏序关系是自反、反对称和可传递的关系。
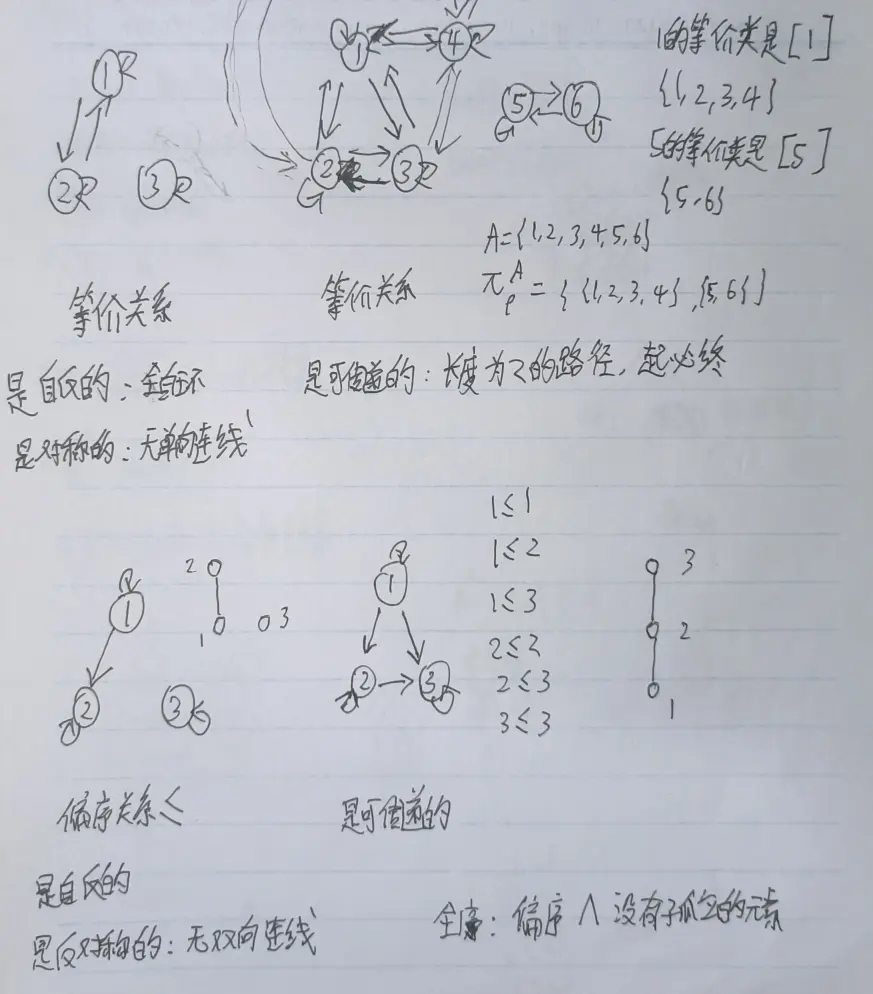
对实数集来说:
- 小于等于关系是自反的。对于所有 a,有 a <= a
- 小于等于关系是非对称的。由 1 <= 2,但 2 不 <= 1
- 小于等于关系是反对称的。如果 a <= b,且 b <= a,那么 a 一定等于 b
- 小于等于关系是可传递的。所以实数集上的 “小于等于” 关系是偏序。偏序用符号 ≤ 表示。
闭包是指,对一个不一定具有某个性质的,集合 A 上的关系 rho,通过并的操作使它具有某个性质。在原来的线里多加几根线
- 自反闭包 r:rho 并上 A 的恒等关系
- 对称闭包 s:rho 并上 rho 的逆关系
- 传递闭包 t:rho 的次方从 1 连并到 A 的基数。次方是同一个关系多次复合,复合是找从起点集合到终点集合的连续路。关系的复合是可结合的
r (rho)、s (rho)、t (rho) 分别是集合 A 上包含 rho 的最小自反 / 对称 / 可传递的关系。
对于一个等价关系,它的某个元素的等价类,从关系图上看,就是这个元素一坨所在的所有元素。等价分划就是把一坨一坨的分开。
{1,2,3}
的所有分划是:{{1,2,3}}、{{1},{2,3}}、{{1,2},{3}}、{{1,3},2}、{{1},{2},{3}}
A 的平凡分划就是 {A},是它上普遍关系导出的等价分划,是最粗的分划。最细的分划就是切成臊子,是恒等关系导出的等价分划。
函数
函数是从集合 A(起点)到集合 B(终点)的一种特殊的关系。任取起点里的一个元素(像源),它保证往终点的某个像引出了有且只有一条线。
从 A 到 B 的:
- 关系,线可以有一对多的;函数,线不能有一对多的
- 关系,定义域是 A 的子集;函数,定义域为 A
函数的定义域是 A(因为是任取),值域是 B 的子集(因为可能引到同一个终点元素身上),值域包是 B。
如果 A 和 B 是可数集,那么值域的元素个数可能等于定义域(双射),可能小于定义域(极端的都引到同一个终点元素身上),不可能大于定义域。
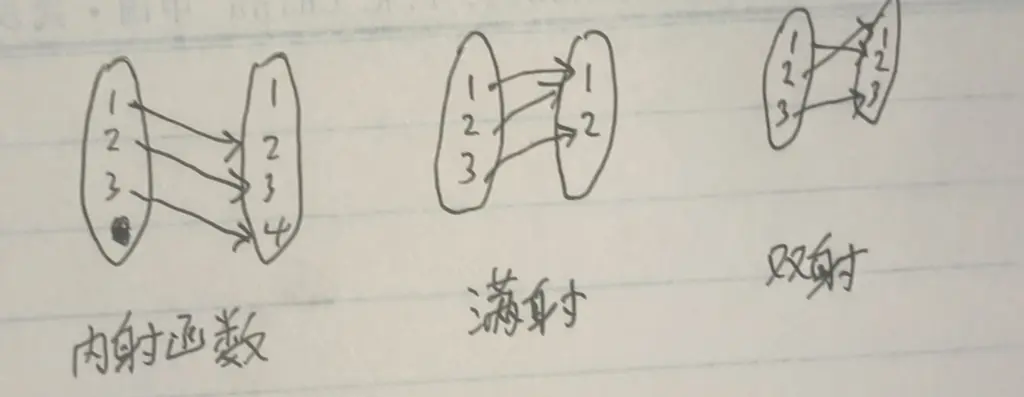
内射的函数是,对于一个函数,任取起点里的两个不等元素,它们两个不会引到终点里的同一个元素上(没有多对一,再加上函数的定义保证它没有一对多,所以都是一对一)。即同一个像源只映射同一个像。A 基数 == 值域元素个数 <= B 基数。当内射的值域取满值域包时,内射变为双射。
满射就是,值域取满值域包。终点的所有元素都被起点连了。A 基数大于等于 B 基数,可能有多对一的情况。
内射且满射,称为双射。双射是一一对应的(内射保证),像和像源的个数相同,且等于 B 的基数(满射保证取满值域包)
幂等函数是指,对一个集合 A 上的函数 f,与自身复合任意次后(>=2 的整数)仍为 f
A 与 B 等势(A~B) <=> 存在从 A 到 B 的双射函数。实数集的所有开区间的子集都和实数集等势,我们都可以画出一个看起来像正切函数的一支的图像,把定义域映射到 R
- 可计数集
- 有限集:元素个数为某个正整数 m,基数是 m。或为空集,基数是 0。如 {1,2,3}
- 可数集(无限的,且可以排成无穷序列的形式):与自然数集
N={0,1,2,3,...} 等势的集合,基数是阿列夫零。如 {2,4,6,8,...} 是 N
的各个元素两倍 + 2 的双射
- 可数集与 [可数集 | 有限集] 的并集是可数集,[有限个 | 可数个] 可数集的并集是可数集
- 有理数集 Q 是可数集,任一个有理数都可以写成分数的形式,分子和分母所有可能的取值都是可数的。任一个有理数都可以写成有限小数或无限循环小数的形式
- 不可数集(无限的)
- 无理数集是不可数的。无理数是无限不循环小数
对于一个集族如 S = {A,B,C,D},如果 A 与 B 的基数都是阿列夫零,C 与 D
的基数都是阿列夫一,那么 S 上存在一个等价关系
{(A,A),(A,B),(B,B),(C,D),(C,C),(D,D)},它的等价分划是 {{A,B},{C,D}},A
的等价类是 {A,B},A 和 B 同基(基数相同)。
二元运算与代数系统
A = {1,2,3}
A^2 = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}
A^3 = {(1,1,1),...}
函数 A^2 -> A:是 A 上的一个二元运算。n 元运算是把 A^n 映射到 A。
关系(或者说函数) {((1,1),2), ((1,2),3)} 不是 A 上的二元运算,因为定义域不等于 A^2,A 上的元素不是都和它自己以及和其他任一个元素起关系了。A 上的二元运算是从 A 的笛卡尔积向 A 的映射,它的定义域里一定有 A 里所有元素的不同排列方式的序偶。
为什么除不是实数集上的二元运算,因为 (n,0) 的结果在 R 里没有对应的像,所以 (n,0) 不在定义域里,而运算要求定义域里一定要有值域包元素的所有序偶。
减是实数集上的二元运算,但不是自然数集上的二元运算,因为 (1,4) 如果有像,那么 -3 是不在自然数集里的。减在实数集上封闭,在自然数集上不封闭。
封闭:对于 A 上的二元运算 ◦,S 是 A 的子集,如果对于所有 S^2 里的元素,在运算之后的结果在 S 里面,那么 ◦ 在 S 上是封闭的。
对于二元运算 *:A^2 -> A:
- 单位元与元素运算,结果为原元素,e * a = a
- 零元与元素运算,结果为零元, z * a = z
- 幂等元和他自身运算的结果不变。二元运算的单位元和零元都是幂等元
- 左单位元和 a 运算,a 不变。a 和右零元运算,结果为右零元
- 不可能同时有不等值的 [左 | 右][单位元 | 零元]
- a 与其右逆元运算,结果是 e
- 当 A 的基数大于 1 时,且存在单位元和零元时,那么它们不会是同一个元素
实数集上的乘法运算,单位元是 1,零元是 0。对于非零元素 a,它的逆元是其倒数
实数集上的加法运算,单位元是 0,没有零元。对于元素 a,它的逆元是其相反数
实数集上的减法运算,右单位元是 0,没有左单位元,没有零元。逆元是根据单位元定义的,所以没有逆元
对于一个元素不多的二元运算,我们可以画出运算表,它的行标为左元素,列标为右元素,内容为运算结果。可以通过运算表里元素排列的形状判断某一个元素是不是单位元或零元。如图所示:
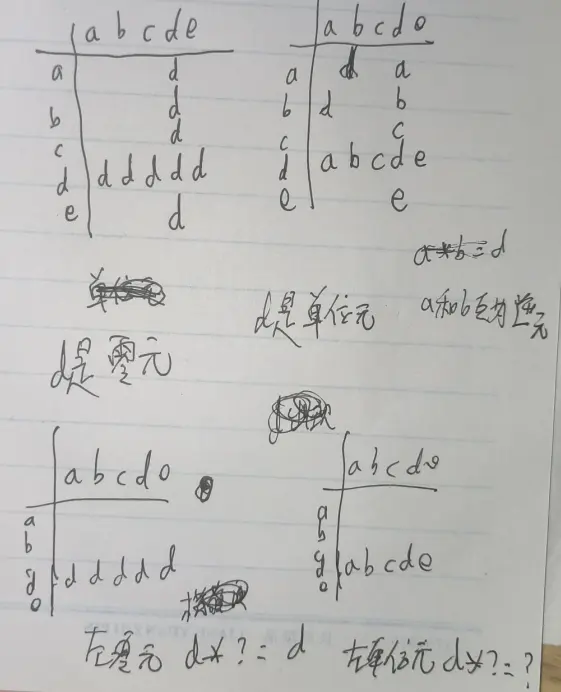
{0,1} 上的:

- 且运算,单位元是 1,零元是 0。且 1 不变,且 0 短路。
- 或运算,单位元是 0,零元是 1。或 0 不变,或 1 短路。
- 蕴含运算,左单位元是 1,右零元是 1
- 等值运算,单位元是 1
<S;o1,o2...> 是代数系统。S 是非空集,称为代数系统的域,on 是一个或多个定义在 S 上的运算(可以不同阶)。
代数系统的基数是 S 的基数,若 S 是有限集,则代数系统是有限代数系统。
整环:对于一个代数系统 <J;+,*>,J 是非空集,+ 和 * 是其上的二元运算,如果同时满足六个性质,则该代数系统为整环:
- + 和 * 都满足交换律
- + 和 * 都满足结合律
- * 对于 + 满足分配律:a*(b+c) = a*b+a*c
- + 和 * 都有单位元
- 任取元素 a 对 + 可逆,a+a 的逆元 = “+ 的单位元”
- 对 * 的消去律:任取非 “+ 的单位元” 的 a,由 a*b = a*c,可得 b=c
对 <{0,1}; 或,且 > 来说:
- 两个运算的交换律、结合律、分配律都满足
- 或的单位元是 0,且的单位元是 1
- 没有对或的可逆性:对 1 来说,不存在它的逆元可以通过与它运算来获得或的单位元 0,所以或是不可逆的。所以该代数系统不是整环
- 有对且的消去律:由:1 且 b = 1 且 c,可得出 b=c,所以满足对且的消去律。
群
对于代数系统 <S;*>,S 是非空集,* 是 S 上的二元运算 S^2 -> S
- 如果 * 是可结合的,则该代数系统为半群
- 若半群有单位元,则该半群为独异点
- 若独异点的域里每个元素都有逆元,则该独异点为群
- 若群的运算 * 是可交换的,则该群为阿贝尔群
命题逻辑
命题:参考洪帆主编的《离散数学基础(第三版)》,并加上了自己的狭隘理解,同时满足以下三条:
- 它是一个陈述句
- 它有一个自带的属性,叫真值,取 \(0\) 或 \(1\)
- 它的真值可以被判断(没有说被谁判断、在什么时间被判断)
2x - 3 = 0
这句话是假的
我们永远没法判断它们的真值是 \(0\) 还是 \(1\)(如果前者是一个陈述句而不是方程,我们不知道 x 是什么东西的。后者……)。所以它们不是命题。
2024 年 1 月 16 号体彩排列三的开奖号码是 703
它是一个命题。它的真值可以被判断,因为这件事已经发生了,但需要我们查询资料。
2024 年 1 月 17 号体彩排列三的开奖号码是 555
> 太阳系外有宇宙人
它们都是命题。它们的真值可以被判断,但不是现在。
命题连结词,一元的只有:否定 \(\neg\),非……。下面都是二元的。
1 | def logic(P: bool, Q: bool) -> bool: |
现在有一份鱼和一份熊掌。作为前件和后件。如果我们吃了,件的真值记为 \(1\),否则记为 \(0\);如果我们满足了(吃好了),复合命题的真值记为 \(1\),否则记为 \(0\)
合取 \(\wedge\) …… 且……:全吃了,我才满足
1 | return P and Q |
析取 \(\vee\) …… 或……(可兼的或):只要有吃的,我就满足
1 | return P or Q |
不可兼的叫异或。区别是:异或的鱼和熊掌只能吃一个,同时吃会生病。
1 | return P ^ Q |
等值 \(\leftrightarrow\) …… 当且仅当……:是异或的对立面:同或、完美主义:要么都吃,要么都不吃,只吃一个我就难受。
1 | return P == Q |
蕴含 \(\rightarrow\) …… 若则……:
现在有【生】和【义】,作为前件和后件。如果我们保留了,件的真值记为 \(1\),否则记为 \(0\);如果我们满足了(垂名了),复合命题的真值记为 \(1\),否则记为 \(0\)
注意:
- 在蕴含的前件为假的情况下,复合命题为真。
- 在蕴含的前件为真的情况下,复合命题的真值为后件的真值。
如果我们把【生】舍了,那还管它义不义,名字直接刻碑上了。或者这样记:如果一个人的前提都搞错了,那就没有必要和他讨论了,你说得都对。
1 | return True if not P else Q |
一个文字游戏:除非 P,否则不 Q
1 | if P: |
就是当且仅当
1 | return P == Q |